题目内容
设集合M={(x,y)|x2+y2≤4},N={(x,y)|(x-1)2+(y-1)2≤r2(r>0)},当M∩N=N时,r的取值范围是
- A.
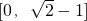
- B.[0,1]
- C.
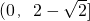
- D.(0,2)
C
分析:由题意可得M、N分别表示两个圆面,且这两个圆相内含或内切,|CO|≤2-r,即 ≤2-r,由此求得r的取值范围.
≤2-r,由此求得r的取值范围.
解答:集合M表示以原点O(0,0)为圆心、半径等于2的圆面(圆及圆的内部),集合N表示以C(1,1)为圆心、半径等于r的圆面(圆及圆的内部).
当M∩N=N时,圆C内含或内切与圆O,故有|CO|≤2-r,即 ≤2-r,∴0<r≤2-
≤2-r,∴0<r≤2- ,
,
故选C.
点评:本题主要考查两圆的位置关系,两圆相内含或内切时,两圆的圆心距小于或等于两圆的半径之差,属于中档题.
分析:由题意可得M、N分别表示两个圆面,且这两个圆相内含或内切,|CO|≤2-r,即
 ≤2-r,由此求得r的取值范围.
≤2-r,由此求得r的取值范围.解答:集合M表示以原点O(0,0)为圆心、半径等于2的圆面(圆及圆的内部),集合N表示以C(1,1)为圆心、半径等于r的圆面(圆及圆的内部).
当M∩N=N时,圆C内含或内切与圆O,故有|CO|≤2-r,即
 ≤2-r,∴0<r≤2-
≤2-r,∴0<r≤2- ,
,故选C.
点评:本题主要考查两圆的位置关系,两圆相内含或内切时,两圆的圆心距小于或等于两圆的半径之差,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .
,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 . ,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .
,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 . ,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .
,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .