题目内容
设集合 ,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .
,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是 .
【答案】分析:根据题意可把问题转换为圆与直线有交点,即圆心到直线的距离小于或等于半径,进而联立不等式组求得m的范围.
解答:解:依题意可知集合A表示一系列圆内点的集合,集合B表示出一系列直线的集合,要使两集合不为空集,需直线与圆有交点,由 可得m≤0或m≥
可得m≤0或m≥
当m≤0时,有| |>-m且|
|>-m且| |>-m;
|>-m;
则有 -
- m>-m,
m>-m, -
- m>-m,
m>-m,
又由m≤0,则2>2m+1,可得A∩B=∅,
当m≥ 时,有|
时,有| |≤m或|
|≤m或| |≤m,
|≤m,
解可得:2- ≤m≤2+
≤m≤2+ ,1-
,1- ≤m≤1+
≤m≤1+ ,
,
又由m≥ ,则m的范围是[
,则m的范围是[ ,2+
,2+ ];
];
综合可得m的范围是[ ,2+
,2+ ];
];
故答案为[ ,2+
,2+ ].
].
点评:本题主要考查了直线与圆的位置关系.一般是利用数形结合的方法,通过圆心到直线的距离来判断.
解答:解:依题意可知集合A表示一系列圆内点的集合,集合B表示出一系列直线的集合,要使两集合不为空集,需直线与圆有交点,由
 可得m≤0或m≥
可得m≤0或m≥
当m≤0时,有|
 |>-m且|
|>-m且| |>-m;
|>-m;则有
 -
- m>-m,
m>-m, -
- m>-m,
m>-m,又由m≤0,则2>2m+1,可得A∩B=∅,
当m≥
 时,有|
时,有| |≤m或|
|≤m或| |≤m,
|≤m,解可得:2-
 ≤m≤2+
≤m≤2+ ,1-
,1- ≤m≤1+
≤m≤1+ ,
,又由m≥
 ,则m的范围是[
,则m的范围是[ ,2+
,2+ ];
];综合可得m的范围是[
 ,2+
,2+ ];
];故答案为[
 ,2+
,2+ ].
].点评:本题主要考查了直线与圆的位置关系.一般是利用数形结合的方法,通过圆心到直线的距离来判断.

练习册系列答案
相关题目
 , B=
, B= , 函数f(x)=
, 函数f(x)=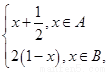 若x
若x
 , 且
, 且 ,则x
,则x B.
B. C.
C. D.
D.
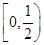 ,
B=
,
B= ,
函数f(x)=
,
函数f(x)= 若
若 ,
且
,
且 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 ,
B=
,
B= ,
函数f(x)=
,
函数f(x)=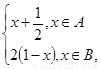 若x
若x
 ,
且f [ f (x
,
且f [ f (x B.
B. C.
C. D.
D.
 ,
B=
,
B= ,
函数f(x)=
,
函数f(x)=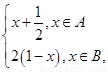 若x
若x
 ,
且f [ f (x
,
且f [ f (x B.
B. C.
C. D.
D.
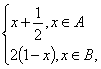 若x
若x