题目内容
某人要制作一个三角形,要求它的三条高的长度分别是 ,则此人 ( )
,则此人 ( )
 ,则此人 ( )
,则此人 ( )| A.不能作出这样的三角形 | B.能作出一个锐角三角形 |
| C.能作出一个直角三角形 | D.能作出一个钝角三角形 |
D
试题分析:分别设出三条高对应的三角形边长,设三角形的面积为k,根据等积法即可用k表示出a,b及c,然后利用余弦定理表示出cosC,把表示出的a,b及c代入即可求出cosC的值,根据cosC的值小于0和C的范围,即可得到C为钝角,从而得到三角形为钝角三角形.。解:设此三角形的三边长分别为a,b及c,则即a=6k,b=10k,c=14k,根据余弦定理得:cosC=
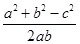 <0,∵C∈(0,π),∴C为钝角,则此人能作出一个钝角三角形.故选D
<0,∵C∈(0,π),∴C为钝角,则此人能作出一个钝角三角形.故选D点评:此题考查了余弦定理,设出三角形的三边,利用等积法表示出三角形三边是本题的突破点,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的内角
的内角 所对的边
所对的边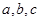 满足
满足 ,且
,且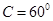 ,则
,则  的值为( )
的值为( )
 1
1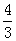
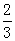
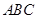 中,
中, ,则
,则 的大小为( )
的大小为( )

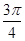
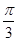
 _________。
_________。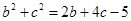 且
且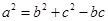 ,则△ABC的面积为( )
,则△ABC的面积为( )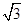
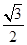
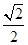
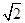
 ∶
∶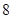 ∶
∶ ,则∠
,则∠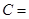 _____________。
_____________。


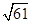
 与圆
与圆 相离,则三条边长分别为
相离,则三条边长分别为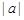 、
、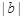 、
、 的三角形是
的三角形是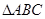 满足:
满足: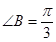 ,
,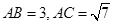 ,则BC的长( )
,则BC的长( )