题目内容
=（
），
=
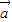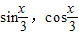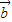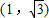，f（x）=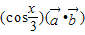
①求f（x）图象对称中心坐标
②若△ABC三边a、b、c满足b2=ac，且b边所对角为x，求x的范围及f（x）值域．
【答案】分析：①利用向量的数量积运算及三角恒等变换公式对解析式进行化简，然后再由解析式求对称中心的坐标
②先由余弦定理表示出角x的余弦，再根据基本不等式求出其取值范围，以此范围做定义域，利用三角函数的性质求出值域．
解答：解：①f（x）=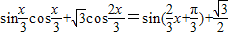
令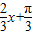
=kπ
∴x=
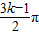，k∈z，
f（x）图象对称中心坐标为：（
，
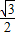），k∈z．
②
∴
∴
＜
∴
＜
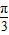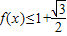
点评：本题考查正弦函数的对称性及求三角函数的值域，解题的关键是对三角函数的解析式进行化简，根据其性质求对称中心的坐标，第二问中利用余弦定理表示出角的函数，再利用基本不等式求出余弦值的范围，知识性很强，是本题中的难点，解题时要认真体会．
②先由余弦定理表示出角x的余弦，再根据基本不等式求出其取值范围，以此范围做定义域，利用三角函数的性质求出值域．
解答：解：①f（x）=
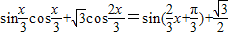
令
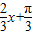=kπ∴x=
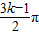，k∈z，f（x）图象对称中心坐标为：（
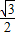，），k∈z．②
∴
∴
＜∴
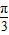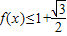
＜点评：本题考查正弦函数的对称性及求三角函数的值域，解题的关键是对三角函数的解析式进行化简，根据其性质求对称中心的坐标，第二问中利用余弦定理表示出角的函数，再利用基本不等式求出余弦值的范围，知识性很强，是本题中的难点，解题时要认真体会．
练习册系列答案
相关题目