题目内容
已知A(2,0),B(0,2),C(cosα,sinα),且0<α<π(1)若|
| OA |
| OC |
| 7 |
| OB |
| OC |
(2)若AC⊥BC,求tanα的值.
分析:(1)利用向量的坐标运算求出
+
;利用向量模的坐标公式得到三角函数方程,求出α;求出两个向量的夹角.
(2)利用向量的坐标公式求出两个向量的坐标;利用向量垂直的充要条件列出方程求出cosa+sina=
;利用三角函数的平方关系将此等式平方求出cosα-sinα;求出sinα,cosα;利用三角函数的商数关系求出tanα.
| OA |
| OC |
(2)利用向量的坐标公式求出两个向量的坐标;利用向量垂直的充要条件列出方程求出cosa+sina=
| 1 |
| 2 |
解答:解:(1)∵
+
=(2+cosα,sinα),|
+
|=
∴(2+cosα)2+sin2a=7,
∴cosα=
又α∈(0,π),
∴α=
,即∠AOC=
又∠AOB=
,∴OB与OC的夹角为
;
(2)
=(cosα-2,sinα),
=(cosα,sinα-2),
∵AC⊥BC,∴
•
=0,cosα+sinα=
①
∴(cosα+sinα)2=
,∴2sinαcosα=-
∵α∈(0,π),∴α∈(
,π),
又由(cosα-sinα)2=1-2sinαcosα=
,cosα-sinα<0,
∴cosα-sinα=-
②由①、②得cosα=
,sinα=
,
从而tanα=-
.
| OA |
| OC |
| OA |
| OC |
| 7 |
∴(2+cosα)2+sin2a=7,
∴cosα=
| 1 |
| 2 |
∴α=
| π |
| 3 |
| π |
| 3 |
又∠AOB=
| π |
| 2 |
| π |
| 6 |
(2)
| AC |
| BC |
∵AC⊥BC,∴
| AC |
| BC |
| 1 |
| 2 |
∴(cosα+sinα)2=
| 1 |
| 4 |
| 3 |
| 4 |
∵α∈(0,π),∴α∈(
| π |
| 2 |
又由(cosα-sinα)2=1-2sinαcosα=
| 7 |
| 4 |
∴cosα-sinα=-
| ||
| 2 |
1-
| ||
| 4 |
1+
| ||
| 4 |
从而tanα=-
4+
| ||
| 3 |
点评:本题考查向量模的坐标公式、考查向量垂直的充要条件、考查三角函数的平方关系、商数关系、
考查cosα+sinα、cosα-sinα、2sinαcosα三者知二求一.
考查cosα+sinα、cosα-sinα、2sinαcosα三者知二求一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知A(2,0),B(3,3),直线l⊥AB,则直线l的斜率k=( )
| A、-3 | ||
| B、3 | ||
C、-
| ||
D、
|
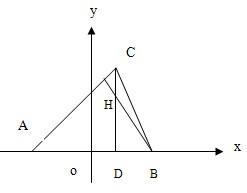 如图,在△ABC中,已知A(-
如图,在△ABC中,已知A(- 如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且