Question

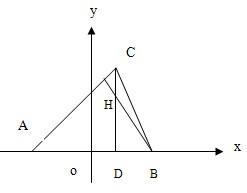如图，在△ABC中，已知A（-

2

，0），B（

2

，0），CD⊥AB于D，△ABC的垂心为H，且

CD

=2

CH

．
（Ⅰ）求点H的轨迹方程；
（Ⅱ）若过定点F（0，2）的直线交曲线E于不同的两点G，H（点G在F，H之间），且满足

FG

=λ

FH

，求λ的取值范围．

Answer 1

分析：（Ⅰ）设点H的坐标为（x，y），C点坐标为（x，m），则D（x，0），

CD

=(0，-m)，

CH

=(0，y-m)，

CD

=2

CH

，m=2y，故C点为（x，2y），由此能求出点H的轨迹方程．
（Ⅱ）直线GH斜率存在时，设G（x₁，y₁），H（x₂，y₂），

FG

=λ

FH

，（x₁，y₁-2）=λ（x₂，y₂-2），x₁=λx₂，x₁+x₂=（1+λ）x₂，x₁x₂=λx₂²，由此知

1

3

＜λ＜ 3，由0＜λ＜1，知

1

3

＜λ＜1．当直线GH斜率不存在时，方程为x=0，

FG

=

1

3

FH

，λ=

1

3

，故所求的λ的取值范围是[

1

3

，1)．．

解答：解：（Ⅰ）设点H的坐标为（x，y），C点坐标为（x，m），则D（x，0），
∴

CD

=(0，-m)，

CH

=(0，y-m)，

CD

=2

CH

，
∴m=2y，故C点为（x，2y），
∵

AC

•

BH

=0，
∴(x+

2

，2y)•(x-

2

，y)=0（2分）
故点H的轨迹方程为

x2

2

+y2=1(y≠0)．（6分）
（Ⅱ）直线GH斜率存在时，设G（x₁，y₁），H（x₂，y₂），
∵

FG

=λ

FH

，
∴（x₁，y₁-2）=λ（x₂，y₂-2），
∴x₁=λx₂，x₁+x₂=（1+λ）x₂，x₁x₂=λx₂²，
∴(

x1+x2

1+λ

)2=x22=

x1x2

λ

，
∴

( -4k 1 2 +k2 )2

(1+λ)2

=

3 1 2 +k2

λ

，整理，得

16

3( 1 2k2 +1)

=

(1+λ)2

λ

，
∵k2＞

3

2

，∴4＜

16

3 2k2 +3

＜

16

3

，∴4＜λ+

1

λ

+2＜

16

3

，
∴

1

3

＜λ＜ 3，
又∵0＜λ＜1，∴

1

3

＜λ＜1．
当直线GH斜率不存在时，方程为x=0，

FG

=

1

3

FH

，λ=

1

3

，
∴

1

3

≤λ＜1．
故所求的λ的取值范围是[

1

3

，1)．．

点评：本题考查直线和圆锥曲线的位置关系，解题时要认真审题，提高解题能力和解题时技巧，注意合理地进行等价转化．