题目内容
已知A(2,0),B(3,3),直线l⊥AB,则直线l的斜率k=( )
| A、-3 | ||
| B、3 | ||
C、-
| ||
D、
|
分析:根据经过两点的直线的斜率公式,算出直线AB的斜率为3,再由垂直的两直线的斜率关系式加以计算,即可得到直线l的斜率k的值.
解答:解:∵A(2,0),B(3,3),
∴直线AB的斜率k'=
=3.
又∵直线l⊥AB,∴直线l的斜率与AB的斜率之积为-1,
即k•k'=-1,解之得k=
=-
.
故选:C
∴直线AB的斜率k'=
| 0-3 |
| 2-3 |
又∵直线l⊥AB,∴直线l的斜率与AB的斜率之积为-1,
即k•k'=-1,解之得k=
| -1 |
| k′ |
| 1 |
| 3 |
故选:C
点评:本题给出A、B两点的坐标,求与直线AB垂直的直线l的斜率k.着重考查了直线的斜率公式与直线的位置关系及其表示式等知识,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
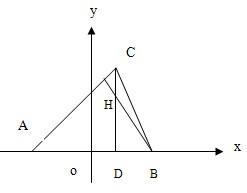 如图,在△ABC中,已知A(-
如图,在△ABC中,已知A(- 如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且