题目内容
在 中,
中, 分别是角
分别是角 的对边,
的对边, 为
为 的面积,若
的面积,若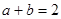 ,且
,且
(1).求 的值; (2).求
的值; (2).求 的最大值。
的最大值。
(1)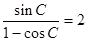 ;(2)
;(2)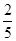
解析试题分析:(1)由 和余弦定理得,
和余弦定理得,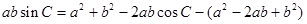 =
=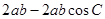
故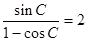 4分
4分
(2)由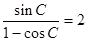 得,
得,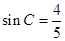
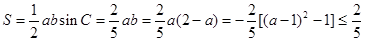 ,
,
当且仅当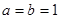 时,面积最大。 4分
时,面积最大。 4分
考点:本题考查了余弦定理及二次函数的最值
点评:熟练运用余弦定理及其变形是解决此类问题的关键,另外还要求学生掌握常见最值的求法

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 中,其中
中,其中 为定点,
为定点, 为动点,满足
为动点,满足 .
. 与
与 的关系式;
的关系式; 的面积分别为
的面积分别为 和
和 ,求
,求 的最大值,以及此时凸四边形
的最大值,以及此时凸四边形 中,已知
中,已知 ,D是BC边上一点,AD=10,AC=14,DC=6,求AB的长.
,D是BC边上一点,AD=10,AC=14,DC=6,求AB的长.
 是锐角三角形,
是锐角三角形, 分别是内角A、B、C所对边长,并且
分别是内角A、B、C所对边长,并且 .
. ;
; ,且
,且 ,求边
,求边 .
. 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知向量
,已知向量 ,且
,且 .
. ,
, ,求△ABC的面积.
,求△ABC的面积. 的方向追赶渔船乙,刚好用2小时追上。
的方向追赶渔船乙,刚好用2小时追上。
 的值。
的值。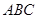 内的空地上植造“绿地
内的空地上植造“绿地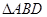 ”,其中
”,其中 ,
,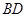 长可根据需要进行调节(
长可根据需要进行调节(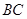 足够长),现规划在
足够长),现规划在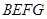 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积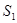 与种花的面积
与种花的面积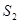 的比
的比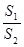 为
为 ,
,
 ,将
,将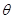 的函数关系;
的函数关系;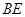 为多长时,
为多长时, 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 ,
, ,
, ,已知
,已知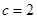 ,
,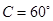
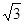 ,求
,求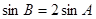 ,求
,求 ,
, ,B=45°求A、C及c
,B=45°求A、C及c