题目内容
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=100.
(Ⅰ)求数列{bn}的通项bn;
(Ⅱ)设数列{an}的通项an=lg(1+![]() ),记Sn是数列{an}的前n项和,试比较Sn与
),记Sn是数列{an}的前n项和,试比较Sn与![]() lgbn+1的大小,并证明你的结论.
lgbn+1的大小,并证明你的结论.
(Ⅰ)设数列{bn}的公差为d,由题意得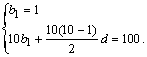
解得![]() ∴bn=2n-1.?
∴bn=2n-1.?
(Ⅱ)由bn=2n-1,知?
Sn=lg(1+1)+lg(1+![]() )+……+lg(1+
)+……+lg(1+![]() )
)
=lg[(1+1)(1+![]() )……(1+
)……(1+![]() )],?
)],?
![]() lgbn+1=lg
lgbn+1=lg![]() .?
.?
因此要比较Sn与![]() lgbn+1的大小,可先比较(1+1)(1+
lgbn+1的大小,可先比较(1+1)(1+![]() )……(1+
)……(1+![]() )与
)与![]() 的大小.?
的大小.?
取n=1有(1+1)>![]() ,?取n=2有(1+1)(1+
,?取n=2有(1+1)(1+![]() )>
)>![]() ……
……
由此推测(1+1)(1+![]() )……(1+
)……(1+![]() )>
)>![]() .①若①式成立,则由对数函数性质
.①若①式成立,则由对数函数性质
可断定:Sn>![]() lgbn+1.?
lgbn+1.?
下面用数学归纳法证明①式.?
(i)当n=1时已验证①式成立.?
(ii)假设当n=k(k≥1)时,①式成立,即(1+1) (1+![]() )……(1+
)……(1+![]() )>
)>![]() .?
.?
那么,当n=k+1时,(1+1) (1+![]() )……(1+
)……(1+![]() )
)![]() >
>![]() (1+
(1+![]() )
)
=![]() (2k+2),?
(2k+2),?
∵[![]() (2k+2)]2-[
(2k+2)]2-[![]() ]2=
]2=![]() =
=![]() >0
>0
∴![]() (2k+2)>
(2k+2)>![]() =
=![]() .
.
因而(1+1)(1+![]() )……(1+
)……(1+![]() )(1+
)(1+![]() )>
)>![]() .?
.?
这就是说①式当n=k+1时也成立.?
由(i),(ii)知①式对任何正整数n都成立.?
由此证得:Sn>![]() lgbn+1.
lgbn+1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目