题目内容
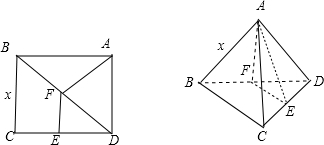
如图，将正方形ABCD沿对角线BD折起，使平面ABD⊥平面CBD，E是CD的中点，那么异面直线AE、BC所成的角的正切值为________．
分析：如图所示：设正方形ABCD的边长为x，取BD的中点为F，先证明∠AEF为异面直线AE、BC所成的角，在直角三角形AEF中，由tan∠AEF=
求出结果．解答：如图所示：设正方形ABCD的边长为x，取BD的中点为F，∵平面ABD⊥平面CBD，E是CD的中点，
故AF⊥平面BCD，EF平行且等于BC的一半，∠AEF为异面直线AE、BC所成的角，且AF=
，EF=
．直角三角形AEF中，tan∠AEF=
=，故答案为
．
点评：本题主要考查异面直线所成的角的定义和求法，图形的翻折问题，解直角三角形，找出两异面直线所成的角，是解题的关键，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
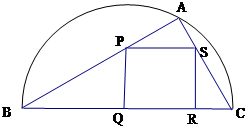如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC的内接正方形PQRS为一水池，△ABC外的地方种草，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值
如图，已知正方形ABCD的边长为2，沿对角线AC将三角形ADC折起，使平面ADC与平面ABC垂直，折叠后B、D两点的距离是（ ）
．