题目内容
如图1所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1,AD1于点B1,P,作CC1∥AA1,分别交A1D1,AD1于点C1,Q,将该正方形沿BB1,CC1折叠,使得DD1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
(Ⅰ)求证:AB⊥平面BCC1B1;
(Ⅱ)求四棱锥A-BCQP的体积;

(Ⅰ)求证:AB⊥平面BCC1B1;
(Ⅱ)求四棱锥A-BCQP的体积;

分析:(1)根据折叠前后的线段长度,得出AB2+BC2=AC2,所以AB⊥BC,因为四边形ADD1A1为正方形,AA1∥BB1,所以AB⊥BB1,可以证出AB⊥平面BCC1B1.
(2)由(1)AB为四棱锥A-BCQP的高.四边形BCQP为直角梯形,利用锥体体积计算公式计算即可.
(2)由(1)AB为四棱锥A-BCQP的高.四边形BCQP为直角梯形,利用锥体体积计算公式计算即可.
解答:(本小题满分14分)
(Ⅰ)证明:在正方形ADD1A1中,因为CD=AD-AB-BC=5,
所以三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.
因为AB=3,BC=4,所以AB2+BC2=AC2,所以AB⊥BC.…(2分)
因为四边形ADD1A1为正方形,AA1∥BB1,所以AB⊥BB1,而BC∩BB1=B,
所以AB⊥平面BCC1B1. …(7分)
(Ⅱ)解:因为AB⊥平面BCC1B1,
所以AB为四棱锥A-BCQP的高.
因为四边形BCQP为直角梯形,且BP=AB=3,CQ=AB+BC=7,
所以梯形BCQP的面积为SBCQP=
(BP+CQ)×BC=20.
所以四棱锥A-BCQP的体积VA-BCQP=
SBCQP×AB=20. …(14分)
(Ⅰ)证明:在正方形ADD1A1中,因为CD=AD-AB-BC=5,
所以三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.
因为AB=3,BC=4,所以AB2+BC2=AC2,所以AB⊥BC.…(2分)
因为四边形ADD1A1为正方形,AA1∥BB1,所以AB⊥BB1,而BC∩BB1=B,
所以AB⊥平面BCC1B1. …(7分)
(Ⅱ)解:因为AB⊥平面BCC1B1,
所以AB为四棱锥A-BCQP的高.
因为四边形BCQP为直角梯形,且BP=AB=3,CQ=AB+BC=7,
所以梯形BCQP的面积为SBCQP=
| 1 |
| 2 |
所以四棱锥A-BCQP的体积VA-BCQP=
| 1 |
| 3 |
点评:本题主要考查空间几何体体积计算,线线垂直,线面垂直的定义,性质、判定,考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
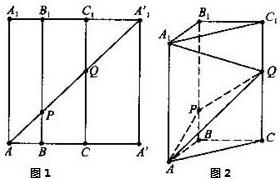 如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,请在图2中解决下列问题:
如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,请在图2中解决下列问题: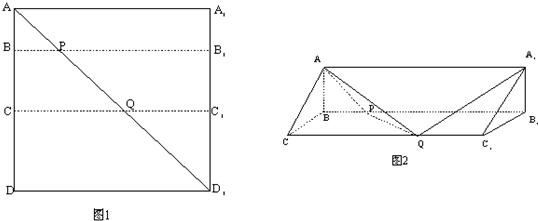
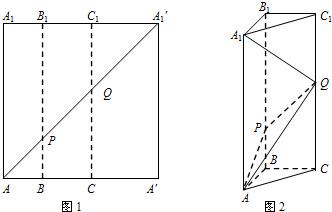 如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1. 如图1所示,在边长为
如图1所示,在边长为