题目内容
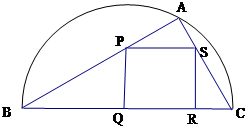 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值| S1 | S2 |
(1)试用a,θ表示S1和S2;
(2)若a为定值,当θ为何值时,“规划合理度”最小?并求出这个最小值.
分析:(1)据题知三角形ABC为直角三角形,根据三角函数分别求出AC和AB,求出三角形ABC的面积S1;设正方形PQRS的边长为x,利用三角函数分别表示出BQ和RC,利用BQ+QR+RC=a列出方程求出x,算出S2;
(2)由比值
称为“规划合理度”,可设t=sin2θ来化简求出S1与S2的比值,利用三角函数的增减性求出比值的最小值即可求出此时的θ.
(2)由比值
| S1 |
| S2 |
解答:解:(1)在Rt△ABC中,AB=acosθ,AC=asinθ,S1=
AB•AC=
a2sinθcosθ(3分)
设正方形的边长为x则BP=
,AP=xcosθ,
由BP+AP=AB,得
+xcosθ=acosθ,故x=
所以S2=x2=(
)2(6分)
(2)
=
•
=
=
+
sin2θ+1,(8分)
令t=sin2θ,因为0<θ<
,
所以0<2θ<π,则t=sin2θ∈(0,1](10分)
所以
=
+
t+1=g(t),g′(t)=-
+
<0,
所以函数g(t)在(0,1]上递减,(11分)
因此当t=1时g(t)有最小值g(t)min=g(1)=
,
此时sin2θ=1,θ=
所以当θ=
时,“规划合理度”最小,最小值为
.(12分)
| 1 |
| 2 |
| 1 |
| 2 |
设正方形的边长为x则BP=
| x |
| sinθ |
由BP+AP=AB,得
| x |
| sinθ |
| asinθcosθ |
| 1+sinθcosθ |
所以S2=x2=(
| asinθcosθ |
| 1+sinθcosθ |
(2)
| S1 |
| S2 |
| 1 |
| 2 |
| (1+sinθcosθ)2 |
| sinθcosθ |
(1+
| ||
| sin2θ |
| 1 |
| sin2θ |
| 1 |
| 4 |
令t=sin2θ,因为0<θ<
| π |
| 2 |
所以0<2θ<π,则t=sin2θ∈(0,1](10分)
所以
| S1 |
| S2 |
| 1 |
| t |
| 1 |
| 4 |
| 1 |
| t2 |
| 1 |
| 4 |
所以函数g(t)在(0,1]上递减,(11分)
因此当t=1时g(t)有最小值g(t)min=g(1)=
| 9 |
| 4 |
此时sin2θ=1,θ=
| π |
| 4 |
所以当θ=
| π |
| 4 |
| 9 |
| 4 |
点评:考查学生会根据实际问题选择合适的函数关系的能力,以及在实际问题中建立三角函数模型的能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
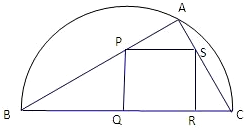 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=20米,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=20米,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值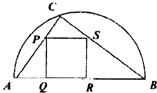 如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值
如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值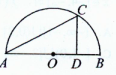 如图,某小区准备绿化一块直径为AB的半圆形空地,O为圆心,C为圆周上一点,CD⊥AB于D,△ACD内为一水池,△ACD外栽种花草,若AB=100米,∠CAB=θ,y=AC+CD.
如图,某小区准备绿化一块直径为AB的半圆形空地,O为圆心,C为圆周上一点,CD⊥AB于D,△ACD内为一水池,△ACD外栽种花草,若AB=100米,∠CAB=θ,y=AC+CD.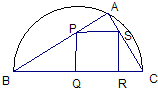 (2007•杨浦区二模)如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
(2007•杨浦区二模)如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值