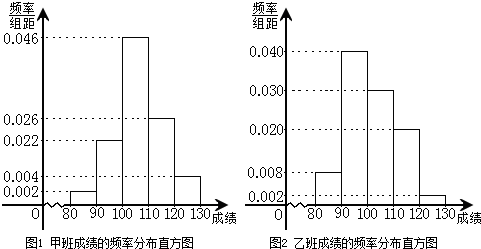
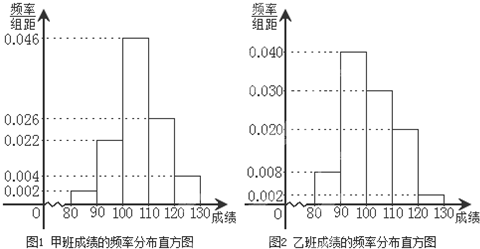
题目内容
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
乙班
(1)现从甲班成绩位于90到100内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
(2)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;
(3)完成下面2×2列联表,你认为在犯错误的概率不超过0.025的前提下,“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由.
附:
甲班
| 成绩 | 2a=6,
|
a=3,c=
|
|
|
△=144k2-12(1+3k2)>0, | |||||||||||||||||||||
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | k2>
|
A(x1,y1),B(x2,y2) | x1+x2=
|
y1+y2=k(x1+x2)-4=k•
|
E(
| ||||||||||||||
| 频数 | 1 | 11 | 23 | 13 | 2 |
(2)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;
(3)完成下面2×2列联表,你认为在犯错误的概率不超过0.025的前提下,“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由.
| 成绩小于100分 | 成绩不小于100分 | 合计 | |||||||
| 甲班 |
|
26 | 50 | ||||||
| 乙班 | 12 | k=±1 | 50 | ||||||
| 合计 | 36 | 64 | 100 |
| x-y-2=0或x+y+2=0. | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | ||
a=
|
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析:(1)由3组数据的存在差异,故应选择分层抽样,先计算出抽样比,进而可计算出各组抽取人数;
(2)累加各组组中与频率的积,可估算出乙班的平均成绩,进而得到两班平均成绩的差;
(3)由已知中表格中的数据,求出甲乙两班成绩小于100和不小于100的人数后,直接代入公式计算,算出数据后与5.024进行比较,可得结论.
(2)累加各组组中与频率的积,可估算出乙班的平均成绩,进而得到两班平均成绩的差;
(3)由已知中表格中的数据,求出甲乙两班成绩小于100和不小于100的人数后,直接代入公式计算,算出数据后与5.024进行比较,可得结论.
解答:解:(1)由于[90,120)内共有3级数据,三段成绩有明显的差异,故用分层抽样的方法更合理;
在[90,100),[100,110),[110,120),共有20+15+10=45人,从中抽取9人
抽样比k=
=
在[90,100)中应抽取20×
=4人,
在[100,110)中应抽取15×
=3人,
在[110,120)中应抽取10×
=2人,
(2)估计乙班的平均分数为
乙=85×
+95×
+105×
+115×
+125×
=105.8
故两班的平均分相差约为4分
(3)由已知中
甲班
乙班
可得2×2列联表如下:
则K2=
≈6.25>5.024,
由附表:
可得所以有97.5%的把握认为这两个班在这次测试中成绩的差异与实施课题实验有关.
即在犯错误的概率不超过0.025的前提下,这两个班在这次测试中成绩的差异与实施课题实验有关
在[90,100),[100,110),[110,120),共有20+15+10=45人,从中抽取9人
抽样比k=
| 9 |
| 45 |
| 1 |
| 5 |
在[90,100)中应抽取20×
| 1 |
| 5 |
在[100,110)中应抽取15×
| 1 |
| 5 |
在[110,120)中应抽取10×
| 1 |
| 5 |
(2)估计乙班的平均分数为
. |
| x |
| 1 |
| 50 |
| 11 |
| 50 |
| 23 |
| 50 |
| 13 |
| 50 |
| 2 |
| 50 |
故两班的平均分相差约为4分
(3)由已知中
甲班
| 成绩 | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) |
| 频数 | 1 | 11 | 23 | 13 | 2 |
| 成绩小于100 | 成绩不小于100分 | 合计 | |
| 甲班 | 24 | 26 | 50 |
| 乙班 | 12 | 38 | 50 |
| 合计 | 36 | 64 | 100 |
| 100×(24×38-26×12)2 |
| 50×50×36×64 |
由附表:
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
即在犯错误的概率不超过0.025的前提下,这两个班在这次测试中成绩的差异与实施课题实验有关
点评:本题考查了独立性检验,我们可以利用临界值的大小来决定是否拒绝原来的统计假设,若值较大就拒绝假设,即拒绝两个事件无关.

练习册系列答案
相关题目