题目内容
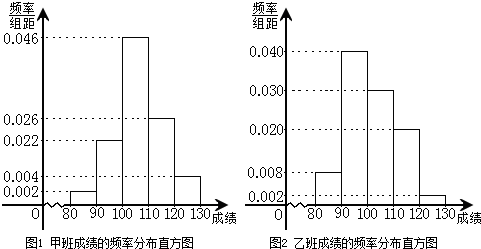
某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图:
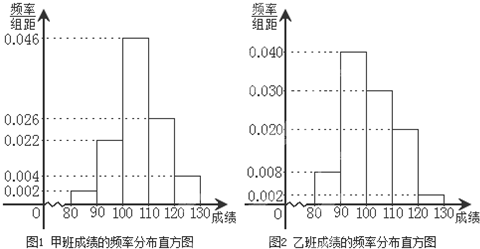
(1)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
(2)根据所给数据可估计在这次测试中,甲班的平均分是105.8,请你估计乙班的平均分,并计算两班平均分相差几分?
附:K2=
,其中n=a+b+c+d

(1)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
| 成绩小于100分 | 成绩不小于100分 | 合计 | |
| 甲班 | a= 12 12 |
b= 38 38 |
50 |
| 乙班 | c=24 | d=26 | 50 |
| 合计 | e= 36 36 |
f= 64 64 |
100 |
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.204 | 6.635 | 7.879 | 10.828 |
分析:(1)由题意,a=0.024×10×50=12,b=50-12=38,e=12+24=36,f=38+26=64,利用公式计算K2,与临界值比较,即可求得结论;
(2)确定乙班各段人数,做成表格,再计算乙班的平均分,利用样本估计总体的方法,估计乙班的平均分,从而可得两班平均分相差多少分.
(2)确定乙班各段人数,做成表格,再计算乙班的平均分,利用样本估计总体的方法,估计乙班的平均分,从而可得两班平均分相差多少分.
解答:解:(1)a=12,b=38,e=36,f=64,…(2分)
K2=
=6.25,…(4分)
∵P( K2>5.204)=0.025,
∴有97.5%的把握认为这两个班在这次测试中成绩的差异与实施课题实验有关”
…(6分)
(2)乙班各段人数分别是:
…(8分)
估计乙班的平均分为:
=101.8…(10分)
两班平均分相差4(分). …(12分)
K2=
| 100(24×38-26×12)2 |
| 50×50×36×64 |
∵P( K2>5.204)=0.025,
∴有97.5%的把握认为这两个班在这次测试中成绩的差异与实施课题实验有关”
…(6分)
(2)乙班各段人数分别是:
| [80,90) | [90,100) | [100,110,) | [110,120) | [120,130) |
| 4 | 20 | 15 | 10 | 1 |
估计乙班的平均分为:
| 85×4+95×20+105×15+115×10+125×1 |
| 50 |
两班平均分相差4(分). …(12分)
点评:本题考查独立性检验,考查频率分布直方图,解题的关键是我们可以利用临界值的大小来决定是否拒绝原来的统计假设,若值较大就拒绝假设,即拒绝两个事件无关.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目