Question

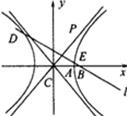已知双曲线C：

x2

a2

+

y2

b2

=1（a＞0，b＞0），B是右顶点，F是右焦点，点A在x轴正半轴上，且满足|

OA

|、|

OB

|、|

OF

|成等比数列，过F作双曲线C在第一、第三象限的渐近线的垂线l，垂足为P．
（1）求证：

PA

•

OP

=

PA

•

FP

；
（2）若l与双曲线C的左、右两支分别相交于点D、E，求双曲线C的离心率e的取值范围．

Answer 1

分析：（1）依题意可表示出l的方程，与渐近线方程联立求得交点P的坐标，根据|

OA

|、|

OB

|、|

OF

|成等比数列，求得A的坐标，进而表示出

PA

，

OP

和

FP

，进而求得

PA

•

OP

和

PA

•

FP

进而可知

PA

•

OP

=

PA

•

FP

．
（2）把直线l的方程与双曲线方程联立，进而根据韦达定理表示出x₁•x₂根据其小于0，求得a和c的不等式关系求得e的范围．

解答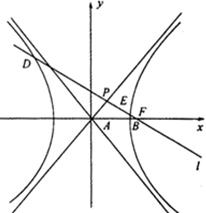：解：（1）l：y=-

a

b

(x-c)，

y=- a b (x-c) y= b a x

解得P(

a2

c

，

ab

c

)．
∵|

OA

|、|

OB

|、|

OF

|成等比数列，
∴A(

a2

c

，0)∴

PA

=(0，-

ab

c

)

OP

=(

a2

c

，

ab

c

)，

FP

=(-

b2

c

，

ab

c

)，
∴

PA

•

OP

=-

a2b2

c2

，

PA

•

FP

=-

a2b2

c2

．
∴

PA

•

OP

=

PA

•

FP

（2）

y=- a b (x-c) b2x2-a2y2=a2b2

，
∴b2x2-

a4

b2

(x-c)2=a2b2．
即(b2-

a4

b2

)x2+2

a4

b2

cx-(

a4c2

b2

+a2b2)=0，
∵x1•x2=

-( a4c2 b2 +a2b2)

b2- a4 b2

＜0，
∴b⁴＞a⁴，即b²＞a²，c²-a²＞a²．∴e²＞2，即e＞

2

．

点评：本题主要考查了直线与圆锥曲线的综合问题．考查了学生综合分析问题和对圆锥曲线基础知识的灵活运用．