题目内容
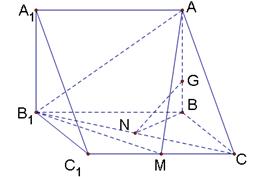
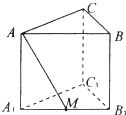
在直三棱柱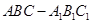 中,
中,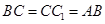 =2 ,
=2 ,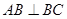 .点
.点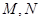 分别是
分别是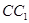 ,
,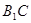 的中点,
的中点,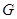 是棱
是棱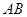 上的动点.
上的动点.
(I)求证: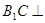 平面
平面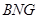 ;
;
(II)若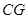 //平面
//平面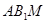 ,试确定
,试确定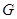 点的位置,
点的位置,
并给出证明;
(III)求二面角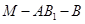 的余弦值.
的余弦值.
 【
【
(1)见解析;(2)见解析;(3)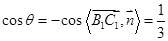 .
.
【解析】本题考查了线面平行与垂直及二面角的求法。第一问抓住线面垂直的判定定理须证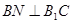 ,
,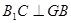 ;第二问先说明
;第二问先说明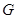 是棱
是棱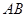 的中点,再,取
的中点,再,取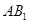 的中点H,证明四边形
的中点H,证明四边形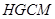 为平行四边形,由线面平行的判定定理得证;第三问利用法向量求二面角
为平行四边形,由线面平行的判定定理得证;第三问利用法向量求二面角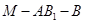 的余弦值,要注意法向量的准确求解和余弦值的正负。
的余弦值,要注意法向量的准确求解和余弦值的正负。
解: (I) 证明:∵在直三棱柱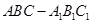 中,
中,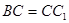 ,点
,点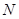 是
是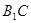 的中点,
的中点,
∴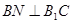 …………………………1分
…………………………1分
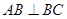 ,
,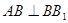 ,
,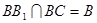
∴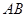 ⊥平面
⊥平面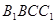 ………………………2分
………………………2分
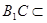 平面
平面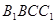
∴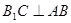 ,即
,即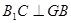 …………………3分
…………………3分
又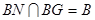
∴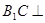 平面
平面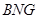 …………………………………4分
…………………………………4分
(II)当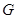 是棱
是棱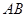 的中点时,
的中点时,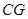 //平面
//平面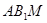 .……………………………5分
.……………………………5分
证明如下:
 连结
连结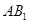 ,取
,取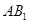 的中点H,连接
的中点H,连接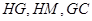 ,
,
则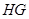 为
为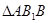 的中位线
的中位线
∴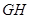 ∥
∥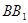 ,
,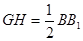 …………………6分
…………………6分
∵由已知条件,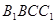 为正方形
为正方形
∴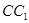 ∥
∥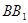 ,
,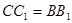
∵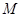 为
为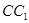 的中点,
的中点,
∴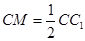 ……………………7分
……………………7分
∴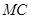 ∥
∥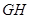 ,且
,且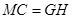
∴四边形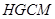 为平行四边形
为平行四边形
∴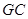 ∥
∥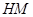
又 ∵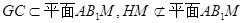
∴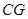 //平面
//平面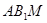 ……………………8分
……………………8分
(III) ∵ 直三棱柱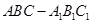 且
且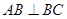
依题意,如图:以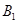 为原点建立空间直角坐标系
为原点建立空间直角坐标系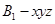 ,……………………9分
,……………………9分


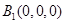 ,
,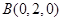 ,
,
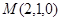
 ,
,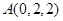 ,
,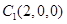
则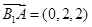 ,
,
设平面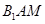 的法向量
的法向量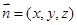 ,
,
则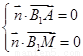 ,即
,即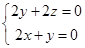 ,
,
令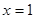 ,有
,有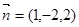 ……………………10分
……………………10分
又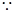 平面
平面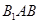 的法向量为
的法向量为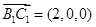 ,
,

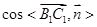 =
=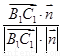 =
=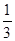 ,
……………………11分
,
……………………11分
设二面角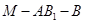 的平面角为
的平面角为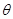 ,且
,且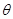 为锐角
为锐角

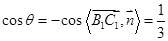 . ……………………12分.
. ……………………12分.

 如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=
如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1= 中,底面
中,底面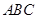 为等边三角形,且
为等边三角形,且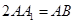 ,
,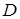 、
、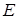 、
、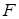 分别是
分别是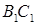 ,
,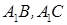 的中点.
的中点.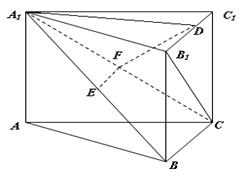
 ∥
∥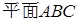 ;
;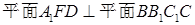 ;
;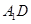 与平面
与平面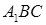 所成的角.
所成的角.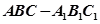 中,
中,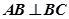 ,
, 为
为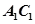 的中点,且
的中点,且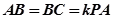 ,
,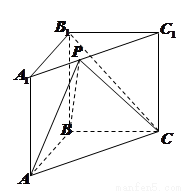
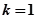 时,求证:
时,求证: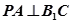 ;
;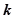 为何值时,直线
为何值时,直线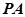 与平面
与平面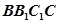 所成的角的正弦值为
所成的角的正弦值为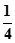 ,并求此时二面角
,并求此时二面角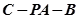 的余弦值。
的余弦值。