题目内容
(2011•江苏二模)在直三棱柱中,AC⊥BC,AC=4,BC=CC1=2,若用平行于三棱柱A1B1C1-ABC的某一侧面的平面去截此三棱柱,使得到的两个几何体能够拼接成长方体,则长方体表面积的最小 值为
24
24
.分析:由图形可以看出,拼接的方法有两种,一种是过AB,AC,A1B1,A1C1的中点截此三棱柱可拼接成一个长方体,其底面是边长为2的正方形,高是2,;另一种是过BC,BA,B1C1,B1A1中点截此三棱柱拼接成一个长方体,此长方体高为2,底面是边长分别为1,4,表面积易求
解答:解:由题意如图,若过AB,AC,A1B1,A1C1的中点截此三棱柱可拼接成一个正方体,其底面是边长为2的正方形,高是2,故其表面积是6×4=24;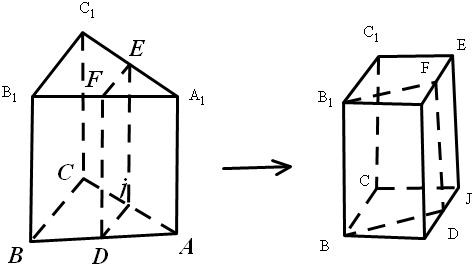
若过BC,BA,B1C1,B1A1中点截此三棱柱拼接成一个长方体,此长方体高为2,底面是边长分别为1,4,故其表面积为2×1×4+2×2×4+2×1×2=28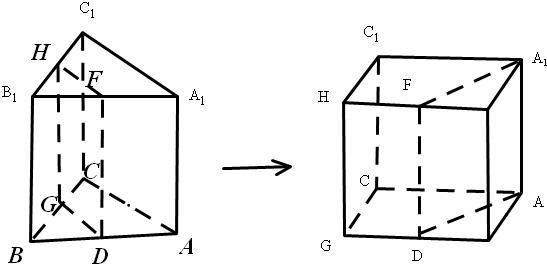
比较知,拼接成长方体的表面积的最小值是24
故答案为24

若过BC,BA,B1C1,B1A1中点截此三棱柱拼接成一个长方体,此长方体高为2,底面是边长分别为1,4,故其表面积为2×1×4+2×2×4+2×1×2=28

比较知,拼接成长方体的表面积的最小值是24
故答案为24
点评:本题考查棱柱的结构特征,解答本题的关键是了解棱柱这个几何体的结构特点,并利用此特点建立起求解问题的模型.

练习册系列答案
相关题目

 (2011•江苏二模)在如图所示的流程图中,输出的结果是
(2011•江苏二模)在如图所示的流程图中,输出的结果是