题目内容
4．设函数y=$\sqrt{lo{g}_{\frac{1}{2}}（x-1）}$的定义域为P，不等式x2-2x≤0的解集为Q，则x∈P是x∈Q的（ ）条件．| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充分必要 | D． | 既不充分也不必要 |
分析 先求出集合P，Q，根据集合之间的关系结合充分必要条件的定义证明即可．
解答 解：由函数y=$\sqrt{lo{g}_{\frac{1}{2}}（x-1）}$，
得：0＜x-1≤1，解得：1＜x≤2，
∴P=（1，2]，
解不等式x2-2x≤0，
得：0≤x≤2，
∴Q=[0，2]，
∴x∈P是x∈Q的充分不必要条件，
故选：A．
点评 本题考查了充分必要条件，考查对数函数的性质，是一道基础题．
练习册系列答案
相关题目
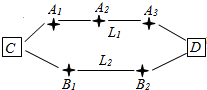小明家住C区，他的学校在D区，从家骑自行车到学校的路有L1、L2．两条路线（如图），路线L1上有A1、A2、A3三个路口，各路口遇到红灯的概率均为$\frac{2}{3}$；L2路线上有B1、B2两个路口，各路口遇到红灯的概率依次为$\frac{3}{4}$、$\frac{3}{5}$．
13．某种产品的广告费支出x与销售额y（单位：万元）之间有如下对应数据：
（Ⅰ）画出散点图；
（Ⅱ）求回归直线方程；（参考数据：$\sum_{i=1}^{5}{{x}_{i}}^{2}$=145，$\sum_{i=1}^{5}{{y}_{i}}^{2}$=13500，$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=1380）
（Ⅲ）试预测广告费支出为10万元时，销售额多大？
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
（Ⅱ）求回归直线方程；（参考数据：$\sum_{i=1}^{5}{{x}_{i}}^{2}$=145，$\sum_{i=1}^{5}{{y}_{i}}^{2}$=13500，$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=1380）
（Ⅲ）试预测广告费支出为10万元时，销售额多大？