题目内容
正方体ABCD—A1B1C1D1的棱长为1,求异面直线A1C1与AB1间的距离.
异面直线A1C1与AB1间距离为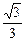 .
.
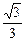 .
. 如图,连结AC1,在正方体AC1中,∵A1C1∥AC,∴A1C1∥平面AB1C,∴A1C1与平面AB1C间的距离等于异面直线A1C1与AB1间的距离.
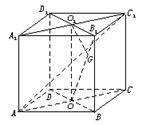
连结B1D1、BD,设B1D1∩A1C1=O1,BD∩AC=O
∵AC⊥BD,AC⊥DD1,∴AC⊥平面BB1D1D
∴平面AB1C⊥平面BB1D1D,连结B1O,则平面AB1C∩平面BB1D1D=B1O
作O1G⊥B1O于G,则O1G⊥平面AB1C
∴O1G为直线A1C1与平面AB1C间的距离,即为异面直线A1C1与AB1间的距离.
在Rt△OO1B1中,∵O1B1=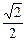 ,OO1=1,∴OB1=
,OO1=1,∴OB1=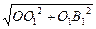 =
= 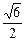
∴O1G=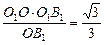 ,即异面直线A1C1与AB1间距离为
,即异面直线A1C1与AB1间距离为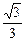 .
.

连结B1D1、BD,设B1D1∩A1C1=O1,BD∩AC=O
∵AC⊥BD,AC⊥DD1,∴AC⊥平面BB1D1D
∴平面AB1C⊥平面BB1D1D,连结B1O,则平面AB1C∩平面BB1D1D=B1O
作O1G⊥B1O于G,则O1G⊥平面AB1C
∴O1G为直线A1C1与平面AB1C间的距离,即为异面直线A1C1与AB1间的距离.
在Rt△OO1B1中,∵O1B1=
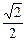 ,OO1=1,∴OB1=
,OO1=1,∴OB1=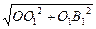 =
= 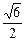
∴O1G=
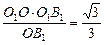 ,即异面直线A1C1与AB1间距离为
,即异面直线A1C1与AB1间距离为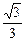 .
.
练习册系列答案
相关题目
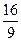 π (B)
π (B)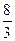 π (C)4π (D)
π (C)4π (D) π
π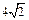 的正三角形
的正三角形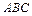 中,
中,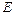 、
、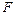 分别为
分别为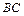 和
和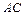 的中点,
的中点,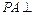 面
面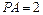 ,设平面
,设平面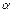 过
过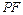 且与
且与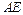 平行。 求
平行。 求
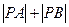 的值为最小
的值为最小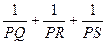 ( )
( )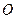 的半径为2,圆
的半径为2,圆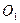 是一小圆,
是一小圆,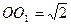 ,A、B是圆
,A、B是圆
 两点,若
两点,若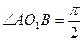 ,则A、B两点间的球面距离为 。
,则A、B两点间的球面距离为 。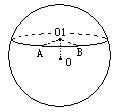
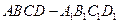 中,
中,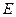
 、
、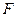 分别为棱
分别为棱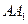 、
、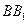 的中点,则点
的中点,则点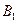 到平面
到平面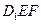 的距离为
的距离为