题目内容
已知A,B两地相距200km,一只船从A地逆流行驶到B地,水流速为8km/h,船在静水中的速度为vkm/h,(8<v≤20),若船每小时的燃料费与在静水中的速度的平方成正比,当v=12km/h时,每小时燃料费为720元.
(1)设船每小时的燃料费为L,求L与v的关系式;
(2)为了使全程燃料费最省,船的实际速度为多少?
(1)设船每小时的燃料费为L,求L与v的关系式;
(2)为了使全程燃料费最省,船的实际速度为多少?
分析:(1)设出正比例函数L=kv2,代入v=12,L=720,求出k,即可得到L与v的关系式;
(2)确定函数解析式,利用导数,确定函数的极值,即为最值,从而可得结论.
(2)确定函数解析式,利用导数,确定函数的极值,即为最值,从而可得结论.
解答:解:(1)设L=kv2,其中k为比例系数
由已知条件,将v=12,L=720代入,得到k=
=5…2
所以L=5v2 (8<v≤20)…3
(2)设全程的燃料费为y,则船每小时的燃料费为5v2,从A地到B地的时间为
故y=5v2×
=
(8<v≤20)…5
∴y′=
…6
令y'=0解得v=0(舍去)或v=16…7
v∈(8,16)时,y′<0,v∈(16,20)时,y′>0
∴v=16时,y取得最小值 …9
∴为了使全程的燃料费最省,船的实际速度应为16km/h.…10
由已知条件,将v=12,L=720代入,得到k=
| 720 |
| 122 |
所以L=5v2 (8<v≤20)…3
(2)设全程的燃料费为y,则船每小时的燃料费为5v2,从A地到B地的时间为
| 200 |
| v-8 |
故y=5v2×
| 200 |
| v-8 |
| 1000v2 |
| v-8 |
∴y′=
| 1000v2-16000v |
| (v-8)2 |
令y'=0解得v=0(舍去)或v=16…7
v∈(8,16)时,y′<0,v∈(16,20)时,y′>0
∴v=16时,y取得最小值 …9
∴为了使全程的燃料费最省,船的实际速度应为16km/h.…10
点评:本题考查函数解析式的确定,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知A,B两地相距150km,某人开汽车以60km/h的速度从A地到达B地,在B地停留1h后再以50km/h的速度返回A地,把汽车离开A地行驶的路程x(km)表示为时间t(h)的函数表达式是( )
| A、x=60t | ||||||||||||
| B、x=60t+50t | ||||||||||||
C、x=
| ||||||||||||
D、x=
|
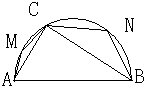 已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.
已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.