题目内容
(本题分12分)
在 中,角
中,角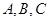 的对边分别为
的对边分别为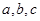 ,
,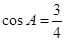 ,
,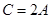
(Ⅰ)求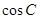 的值;(Ⅱ)若
的值;(Ⅱ)若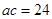 ,求
,求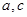 的值.
的值.
【答案】
(1)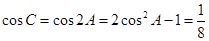 ;(2)
;(2)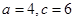 。
。
【解析】本试题主要是考查了解三角形的运用。
(1)根据已知条件先由二倍角公式得到cosC,
(2)然后运用同角公式得到sinA,结合正弦定理得到结论。
解:(1)因为 ,所以
,所以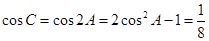 ----------4分
----------4分
(2)在三角形中,因为 ,所以
,所以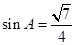 -----------------6分
-----------------6分
因为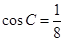 ,所以
,所以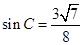 -------------------------8分
-------------------------8分
根据正弦定理得到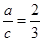 ,又
,又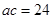
所以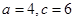 ---------------------------12分
---------------------------12分

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
(本题满分12分)某学校组织的一次篮球定点投篮训练中,规定每人最多投3次:在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次。某学生在A处的命中率q1=0.25,在B处的命中率q2,该同学选择先在A处投一球,以后都在B处投,用X表示该同学投篮结束后所得的总分,其分布列如下:
|
X |
0 |
2 |
3 |
4 |
5 |
|
P |
0.03 |
p1 |
p2 |
p3 |
p4 |
(1)求q2的值;
(2)求随机变量X的均值E(X);
(3)试比较该同学选择都在B处投篮得分超过3分与上述方式投篮得分超过3分的概率的大小。
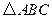 中,内角
中,内角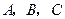 对边的边长分别是
对边的边长分别是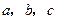 ,且满足
,且满足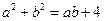 ,
,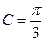 。
。 时,若
时,若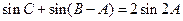 ,求
,求 的一个充要条件。
的一个充要条件。 ,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合)。过D1和CC1的平面与AB交于D。
,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合)。过D1和CC1的平面与AB交于D。