题目内容
已知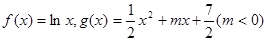 ,直线
,直线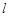 与函数
与函数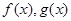 的图像都相切,且与函数
的图像都相切,且与函数 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(1)求直线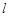 的方程及
的方程及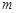 的值;
的值;
(2)若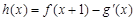 (其中
(其中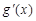 是
是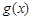 的导函数),求函数
的导函数),求函数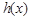 的最大值;
的最大值;
(3)当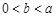 时,求证:
时,求证: .
.
【答案】
(1)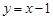 ,m=-2
,m=-2
(2)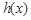 取得最大值
取得最大值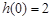
(3)由(Ⅱ)知:当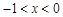 时,
时,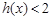 ,即
,即 ,结合单调性来证明。
,结合单调性来证明。
【解析】
试题分析:解:(Ⅰ)依题意知:直线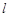 是函数
是函数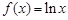 在点
在点 处的切线,故其斜率
处的切线,故其斜率
 ,所以直线
,所以直线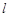 的方程为
的方程为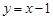 .又因为直线
.又因为直线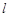 与
与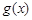 的图像相切,所以由
的图像相切,所以由
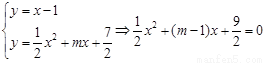 ,
,
得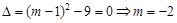 (
(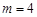 不合题意,舍去); . 4分
不合题意,舍去); . 4分
(Ⅱ)因为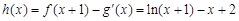 (
( ),所以
),所以
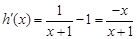 .当
.当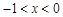 时,
时,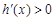 ;当
;当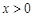 时,
时,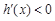 .
.
因此,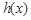 在
在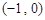 上单调递增,在
上单调递增,在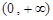 上单调递减.
上单调递减.
因此,当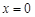 时,
时,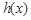 取得最大值
取得最大值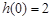 ; . 8分
; . 8分
(Ⅲ)当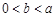 时,
时,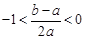 .由(Ⅱ)知:当
.由(Ⅱ)知:当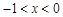 时,
时,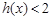 ,即
,即 .因此,有
.因此,有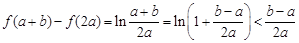 . . 12分
. . 12分
考点:导数的运用
点评:主要是考查了函数的单调性以及不等式的运用,属于基础题。

练习册系列答案
相关题目
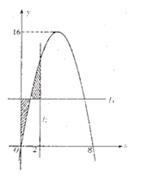 (Ⅰ)求a、b、c的值 (Ⅱ)求阴影面积S关于t的函数
(Ⅰ)求a、b、c的值 (Ⅱ)求阴影面积S关于t的函数
 处取得极值,求实数a的值;
处取得极值,求实数a的值; 与函数
与函数 的图象相切,求实数k的值;
的图象相切,求实数k的值;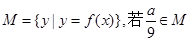 ,求满足条件的实数a的集合.
,求满足条件的实数a的集合. 与函数
与函数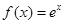 的图象相切,则切点坐标为
的图象相切,则切点坐标为