Question

已知向量

OA

，

OB

的夹角为

π

3

，|

OA

|=4，|

OB

|=1，若点M在直线OB上，则|

OA

-

OM

|的最小值为

 

．

Answer 1

分析：图解法：根据向量减法的三角形法则，|

OA

-

OM

|=|

MA

|，要求|

OA

-

OM

|的最小值，即求|

MA

|的最小值，根据当AM⊥OB时和向量的数量积的几何意义即可求得结果．

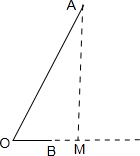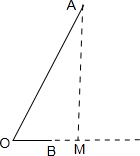解答：解：∵|

OA

-

OM

|=|

MA

|，
∵点M在直线OB上，向量

OA

，

OB

的夹角为

π

3

，|

OA

|=4，|

OB

|=1，
∴当AM⊥OB时，|

OA

-

OM

|=2

3

，
故答案为2

3

．

点评：此题是个基础题．本题考查向量的内积公式与向量加法的三角形法则，本题恰当地利用向量的相关公式灵活变形达到了用已知向量表示未知向量，且求出未知向量的目标．