题目内容
下表是某单位在2013年1—5月份用水量(单位:百吨)的一组数据:
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05,视为“预测可靠”,通过公式得 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
(Ⅱ)从这5个月中任取2个月的用水量,求所取2个月的用水量之和小于7(单位:百吨)的概率
参考公式:回归直线方程是: ,
,
月份 | 1 | 2 | 3 | 4 | 5 |
用水量 | 4 5 | 4 | 3 | 2 5 | 1 8 |
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05,视为“预测可靠”,通过公式得
 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;(Ⅱ)从这5个月中任取2个月的用水量,求所取2个月的用水量之和小于7(单位:百吨)的概率
参考公式:回归直线方程是:
 ,
,
①“预测可靠” ②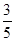
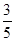
试题分析:(Ⅰ)首先计算
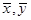 由于已知
由于已知 则 通过
则 通过 计算出
计算出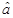 ,从而求出回归方程,再比较回归方程的值与实际值的差的绝对值即可 (Ⅱ)列举法:把所有可能与符合条件的一一列举即可求概率
,从而求出回归方程,再比较回归方程的值与实际值的差的绝对值即可 (Ⅱ)列举法:把所有可能与符合条件的一一列举即可求概率 试题解析:(Ⅰ)由数据,得
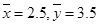 ,且
,且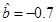
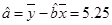 , 所以
, 所以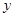 关于
关于 的线性回归方程为
的线性回归方程为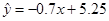
当
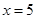 时,得估计值
时,得估计值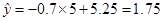 , 而
, 而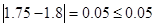 ;
;所以,所得到的回归方程是“预测可靠”的 6分
(Ⅱ)从这5个月中任取2个月,包含的基本事件有以下10个:
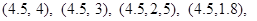
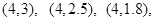
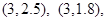
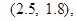
其中所取2个月的用水量之和小于7(百吨)的基本事件有以下6个:

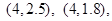
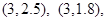
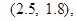
故所求概率
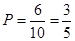 12分
12分
练习册系列答案
相关题目


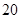



 为优,
为优, 为良,
为良, 为轻度污染,
为轻度污染, 为中度污染,
为中度污染, 为重度污染,300以上为严重污染.2013年5月1日出版的《A市早报》报道了A市2013年4月份中30天的AQI统计数据,下图是根据统计数据绘制的频率分布直方图. 根据图中的信息可以得出A市该月环境空气质量优良的总天数为 .
为重度污染,300以上为严重污染.2013年5月1日出版的《A市早报》报道了A市2013年4月份中30天的AQI统计数据,下图是根据统计数据绘制的频率分布直方图. 根据图中的信息可以得出A市该月环境空气质量优良的总天数为 .
 的数据丢失,则依据此图可得:
的数据丢失,则依据此图可得: 的人数 .
的人数 .
 的样本,其频率分布直方图如图所示,据图估计,样本数据在
的样本,其频率分布直方图如图所示,据图估计,样本数据在 内的频数为
内的频数为
 个同学进行调查,结果显示这些同学的支出都在[10,50)(单 位:元),其中支出在
个同学进行调查,结果显示这些同学的支出都在[10,50)(单 位:元),其中支出在 (单位:元)的同学有67人,其频率分布直方图如图所示,则
(单位:元)的同学有67人,其频率分布直方图如图所示,则