题目内容
下列各组命题中,p是q的充要条件的是
- A.p:两条对角线互相垂直平分,q:四边形是正方形
- B.a,b,c为实数,p:ac2>bc2,q:a>b
- C.p:
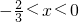 ,q:|2x+1|<|x+1|
,q:|2x+1|<|x+1| - D.p:a>0,q:方程组
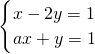 有唯一解
有唯一解
C
分析:若“两条对角线互相垂直平分”成立推不出“四边形是正方形”;反之,若“四边形是正方形”成立推不出“两条对角线互相垂直平分”成立,故A不对;对于B,p能推出q,但q 推不出p,所以B不对,对于C,q:|2x+1|<|x+1|等价于(2x+1)2<(x+1)2等价于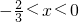 ,所以p是q 的充要条件.对于D,p能推出q但q不能推出p,所以D不对,
,所以p是q 的充要条件.对于D,p能推出q但q不能推出p,所以D不对,
解答:若“两条对角线互相垂直平分”成立推不出“四边形是正方形”;
反之,若“四边形是正方形”成立推不出“两条对角线互相垂直平分”成立,故A不对;
对于B,p能推出q,但q 推不出p,所以B不对,
对于C,q:|2x+1|<|x+1|等价于(2x+1)2<(x+1)2等价于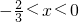 ,所以p是q 的充要条件.
,所以p是q 的充要条件.
对于D,p能推出q但q不能推出p,所以D不对,
故选C.
点评:判断一个命题是另一个命题的什么条件,应该先两边互相推一下,利用充要条件的有关定义进行判断.
分析:若“两条对角线互相垂直平分”成立推不出“四边形是正方形”;反之,若“四边形是正方形”成立推不出“两条对角线互相垂直平分”成立,故A不对;对于B,p能推出q,但q 推不出p,所以B不对,对于C,q:|2x+1|<|x+1|等价于(2x+1)2<(x+1)2等价于
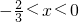 ,所以p是q 的充要条件.对于D,p能推出q但q不能推出p,所以D不对,
,所以p是q 的充要条件.对于D,p能推出q但q不能推出p,所以D不对,解答:若“两条对角线互相垂直平分”成立推不出“四边形是正方形”;
反之,若“四边形是正方形”成立推不出“两条对角线互相垂直平分”成立,故A不对;
对于B,p能推出q,但q 推不出p,所以B不对,
对于C,q:|2x+1|<|x+1|等价于(2x+1)2<(x+1)2等价于
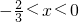 ,所以p是q 的充要条件.
,所以p是q 的充要条件.对于D,p能推出q但q不能推出p,所以D不对,
故选C.
点评:判断一个命题是另一个命题的什么条件,应该先两边互相推一下,利用充要条件的有关定义进行判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目