题目内容

7．函数f（x）=x2+2x-$\frac{{2}^{x}-4}{3}$的零点个数为1．

分析 化简可得3（x+1）2+1=2x，从而作函数的图象求解即可．

解答 解：令f（x）=x2+2x-$\frac{{2}^{x}-4}{3}$=0得，
3（x+1）2+1=2x，
作函数y=3（x+1）2+1与函数y=2x的图象如下，

再作函数y=$\frac{3（x+1）^{2}+1}{10}$与函数y=$\frac{{2}^{x}}{10}$的图象如下，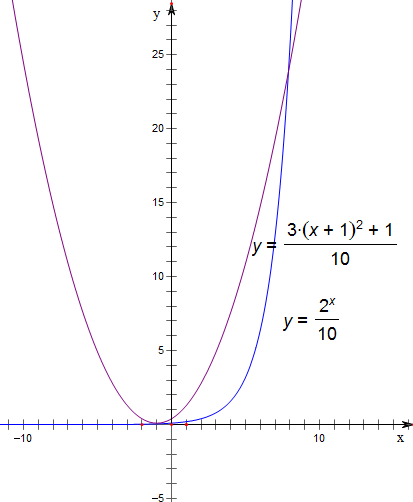

结合图象可知，函数f（x）=x2+2x-$\frac{{2}^{x}-4}{3}$的零点个数为1，
故答案为：1．

点评 本题考查了函数的图象的作法及数形结合的思想应用．属于难题．

练习册系列答案
相关题目
17．化简：（2${a^{\frac{2}{3}}}$${b^{\frac{1}{2}}}$）（-6${a^{\frac{1}{2}}}$${b^{\frac{1}{3}}}$）÷（-3${a^{\frac{1}{6}}}$${b^{\frac{5}{6}}}$）=4a．
18．下列叙述正确的是①②．
①$\overrightarrow{PG}=\frac{1}{3}（\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}）$?G为△ABC的重心，．
②$\overrightarrow{PA}•\overrightarrow{PB}=\overrightarrow{PB}•\overrightarrow{PC}=\overrightarrow{PC}•\overrightarrow{PA}?P$为△ABC的垂心；
③$|\overrightarrow{AB}|\overrightarrow{PC}+|\overrightarrow{BC}|\overrightarrow{PA}+|\overrightarrow{CA}|\overrightarrow{PB}=\overrightarrow 0?P$为△ABC的外心；
④$（\overrightarrow{OA}+\overrightarrow{OB}）•\overrightarrow{AB}=（\overrightarrow{OB}+\overrightarrow{OC}）•\overrightarrow{BC}=（\overrightarrow{OC}+\overrightarrow{OA}）•\overrightarrow{CA}=0$?O为△ABC的内心．
15．已知${（\sqrt{x}-\frac{2}{x^2}）^n}（n∈{N^*}）$的展开式中第五项的系数与第三项的系数之比是10：1
（1）求展开式中各项系数的和
（2）求展开式中含${x^{\frac{3}{2}}}$的项
（3）求展开式中系数最大的项和二项式系数最大的项．
2．关于x的不等式kx2-2x+1＞0的解集是{x∈R|x≠$\frac{1}{k}$}，则k的值是（　　）
A．1B．-1C．±1D．-1≤k≤1
12．在△ABC中，AD是角A的平分线，∠A=60°，AD=AB=2，则CD=$\sqrt{2}$．
19．如图，已知点A∉平面BCD，E，F，G，H分别是AB，BC，CD，DA上的点，且EH与FG交于点P．求证：P在直线BD上．
16．已知$\frac{π}{4}$＜α＜$\frac{π}{2}$，0＜β＜$\frac{π}{3}$，求下列各式的取值范围：
（1）2α+β；
（2）$\frac{α-β}{2}$．
17．U={1，2，3，4，5，6，7，8}，A={1，3，5}，B={1，2，4}，∁UA={2，4，6，7，8}，∁UA∩∁UB={6，7，8}，∁UA∪∁UB={2，3，4，5，6，7，8}．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网