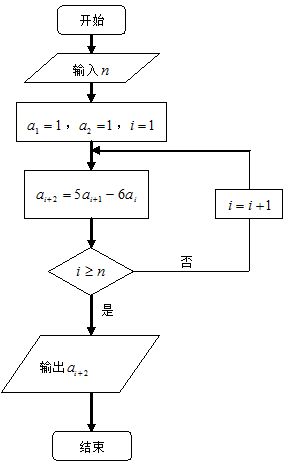题目内容
(14分)
已知数列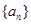 的前
的前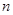 项和为
项和为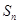 ,且对任意正整数
,且对任意正整数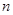 ,有
,有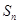 ,
,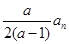 ,
,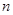 (
(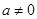 ,
,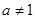 )成等差数列,令
)成等差数列,令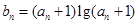 。
。
(1)求数列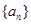 的通项公式
的通项公式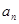 (用
(用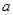 ,
,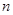 表示)
表示)
(2)当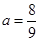 时,数列
时,数列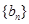 是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
(3)若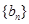 是一个单调递增数列,请求出
是一个单调递增数列,请求出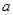 的取值范围。
的取值范围。
【答案】
解:(1)由题意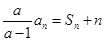 ①
① 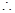
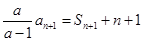 ②
②
 ②-①得
②-①得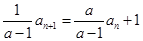 即
即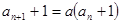 ,
,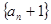 是以
是以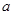 为公比的等比数列。
为公比的等比数列。 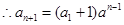 又
又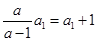
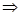
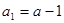
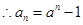
(2) 时,
时,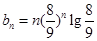 ,
,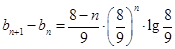
当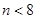 时,
时,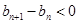 即
即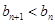 ,
,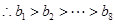
当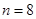 时,
时,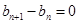 即
即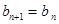 ,
,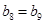
当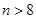 时,
时,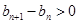 即
即
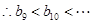 存在最小项且第8项和第9项最小
存在最小项且第8项和第9项最小
(3)由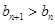 得
得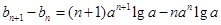
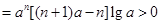
当 时,得
时,得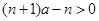 即
即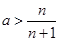 ,显然恒成立
,显然恒成立 

当 时,
时,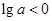
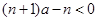 即
即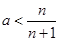
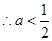
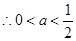
综上,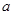 的取值范围为
的取值范围为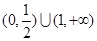 。
。
【解析】略

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 }是首项为
}是首项为 等于1且公比
等于1且公比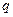 不等于1的等比数列,
不等于1的等比数列, 是其前
是其前 项的和,
项的和, 成等差数列.
成等差数列. ;
; 成等比数列
成等比数列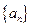 的首项
的首项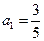 ,
,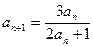 ,其中
,其中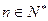 。
。 为等比数列;
为等比数列; 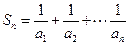 ,若
,若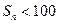 ,求最大的正整数
,求最大的正整数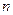 。
。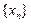 满足
满足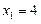 ,
,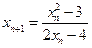 .
.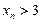 ;
;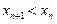 ;
;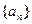 满足如图所示的程序框图.(Ⅰ)写出数列
满足如图所示的程序框图.(Ⅰ)写出数列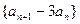 是等比数列,并求
是等比数列,并求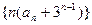 的前
的前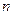 项和
项和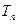 .
.