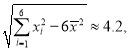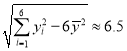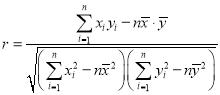题目内容
【题目】已知椭圆C:![]() =1(a>b>0),定义椭圆C上的点M(x0,y0)的“伴随点”为
=1(a>b>0),定义椭圆C上的点M(x0,y0)的“伴随点”为![]() .
.
(1)求椭圆C上的点M的“伴随点”N的轨迹方程;
(2)如果椭圆C上的点(1,![]() )的“伴随点”为(
)的“伴随点”为(![]() ,
,![]() ),对于椭圆C上的任意点M及它的“伴随点”N,求
),对于椭圆C上的任意点M及它的“伴随点”N,求![]() 的取值范围;
的取值范围;
(3)当a=2,b=![]() 时,直线l交椭圆C于A,B两点,若点A,B的“伴随点”分别是P,Q,且以PQ为直径的圆经过坐标原点O,求△OAB的面积.
时,直线l交椭圆C于A,B两点,若点A,B的“伴随点”分别是P,Q,且以PQ为直径的圆经过坐标原点O,求△OAB的面积.
【答案】(1)x2+y2=1,(2)![]() ,(3)
,(3)![]()
【解析】
(1)由 代入椭圆方程即可求得椭圆C上的点M的“伴随点”N的轨迹方程;
代入椭圆方程即可求得椭圆C上的点M的“伴随点”N的轨迹方程;
(2)由题意,求得椭圆的方程,根据向量![]() 的坐标运算,即可求得
的坐标运算,即可求得
(3)求得椭圆方程,设方程为![]() ,代入椭圆方程,利用韦达定理,根据向量数量积的坐标求得
,代入椭圆方程,利用韦达定理,根据向量数量积的坐标求得![]() ,弦长公式及点到直线的距离公式,即可求得
,弦长公式及点到直线的距离公式,即可求得![]() 的面积,直线
的面积,直线![]() 的斜率不存在时,设方程为
的斜率不存在时,设方程为![]() ,代入椭圆方程,即可求得
,代入椭圆方程,即可求得![]() 的面积.
的面积.
(1)设![]() ,由题意
,由题意 ,则
,则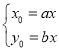 .
.
又![]() ,所以
,所以![]()
![]() .
.
(2)由椭圆C上的点(1,![]() )的“伴随点”为(
)的“伴随点”为(![]() ,
,![]() )
)
则![]() ,得
,得![]() ,又
,又![]() ,则
,则![]() .
.
点![]() ,在椭圆上,
,在椭圆上,![]() ,
,![]() ,且
,且![]()
![]()
由于![]() ,
,![]() 的取值范围是
的取值范围是![]() .
.
(3)设![]() ,则
,则![]()
当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,由
,由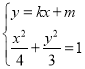 .
.
得![]() .
.
则![]()
![]() ①
①
由以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() 可得:
可得:![]() ,即
,即![]() .
.
又![]()
整理得:![]() ②
②
将①代入②得:![]()
![]() ,则
,则![]() ,
,
所以![]() .
.
又点![]() 到直线
到直线![]() 的距离
的距离![]()
![]()
![]()
所以![]()
当直线![]() 的斜率不存在时,设其方程为
的斜率不存在时,设其方程为![]()
联立椭圆方程得![]()
![]() ,得
,得![]() .
.
解得:![]() ,从而
,从而![]() .
.
![]()
综上:的面积是定值![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目