题目内容
已知α,β是锐角,sinα=x,cosβ=y,cos(α+β)=- ,则y与x的函数关系式为( )
,则y与x的函数关系式为( )A.-
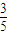
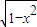 +
+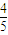 x (
x (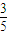 <x<1)
<x<1)B.
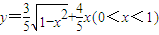
C.
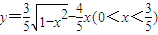
D.
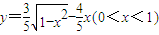
【答案】分析:先根据同角三角函数之间的关系求出cosα以及sin(α+β),再利用两角差的余弦公式即可得到答案.
解答:解:∵知α,β是锐角,sinα=x,cosβ=y,cos(α+β)=-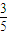 ,
,
∴-sinα=cos(α+90°)<cos(α+β)=-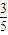 ⇒x>
⇒x>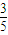 ;
;
∴cosα=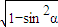 =
=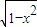 ;
;
sin(α+β)=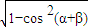 =
=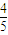 .
.
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=-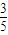
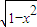 +
+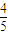 x (
x (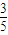 <x<1)
<x<1)
故选:A.
点评:本题主要考查同角三角函数间的基本关系以及角的变换.本题的易错点在于没有找对自变量的取值范围,从而误选答案.
解答:解:∵知α,β是锐角,sinα=x,cosβ=y,cos(α+β)=-
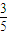 ,
,∴-sinα=cos(α+90°)<cos(α+β)=-
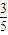 ⇒x>
⇒x>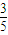 ;
;∴cosα=
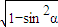 =
=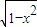 ;
;sin(α+β)=
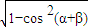 =
=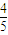 .
.∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=-
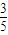
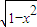 +
+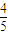 x (
x (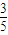 <x<1)
<x<1)故选:A.
点评:本题主要考查同角三角函数间的基本关系以及角的变换.本题的易错点在于没有找对自变量的取值范围,从而误选答案.

练习册系列答案
相关题目