题目内容
已知各项都为正数的等比数列{an},a2=18,a4=8
(1)求此等比数列的通项公式.
(2)判断此数列的第6项是不是等差数列8,
,
,
….的项.
(1)求此等比数列的通项公式.
(2)判断此数列的第6项是不是等差数列8,
| 67 |
| 9 |
| 62 |
| 9 |
| 57 |
| 9 |
分析:(1)设等比数列的公比是q,则根据已知条件有
,解得a1 和q的值,可得等比数列的通项公式.
(2)求得a6=
,等差数列的通项公式为bn=
n+
,令
n+
=
,解得n的值,可得结论.
|
(2)求得a6=
| 32 |
| 9 |
| 5 |
| 9 |
| 77 |
| 9 |
| 5 |
| 9 |
| 77 |
| 9 |
| 32 |
| 9 |
解答:解:(1)设等比数列的公比是q,则根据已知条件有
,
解得
,或
.….3 分
因为该数列各项都为正数,可得
.…(6分)
∴an=27×(
)n-1.…(8分)
(2)由于a6=27×(
)5=
,该等差数列首项是8,公差是-
,
所以通项公式为bn=
n+
.…(12分)
令
n+
=
,解得n=9,故
是这个等差数列的项.…(14分)
|
解得
|
|
因为该数列各项都为正数,可得
|
∴an=27×(
| 2 |
| 3 |
(2)由于a6=27×(
| 2 |
| 3 |
| 32 |
| 9 |
| 5 |
| 9 |
所以通项公式为bn=
| 5 |
| 9 |
| 77 |
| 9 |
令
| 5 |
| 9 |
| 77 |
| 9 |
| 32 |
| 9 |
| 32 |
| 9 |
点评:本题主要考查等比数列的定义和性质,等比数列的通项公式的应用,属于基础题.

练习册系列答案
相关题目
 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈ ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是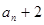 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈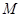 ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 是an+2 和an的等比中项.
是an+2 和an的等比中项. +
+ +…+
+…+ <1;
<1; 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个?