题目内容
(本小题满分12分)
已知A(-3,0),B(3,0),三角形PAB的内切圆的圆心M在直线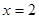 上移动。
上移动。
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)某同学经研究作出判断,曲线C在P点处的切线恒过点M,试问:其判断是否正确?若正确,请给出证明;否则说明理由。
【答案】
(Ⅰ)
(Ⅱ)此同学的判断是正确的,证明见解析
【解析】
(Ⅰ)设 ,三角形PAB的内切圆M与PA、PB、AB的切点分别为
,三角形PAB的内切圆M与PA、PB、AB的切点分别为
E、F、H,则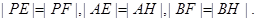

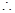 P点的轨迹C为以A、B为焦点的双曲线的右支(除去顶点)
P点的轨迹C为以A、B为焦点的双曲线的右支(除去顶点)
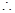 曲线C的方程为
曲线C的方程为
(Ⅱ)此同学的判断是正确的
设P点处曲线的切线交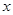 轴于点Q,下证:PQ平分
轴于点Q,下证:PQ平分
不妨设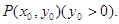
 当
当 时,曲线C满足
时,曲线C满足
 ,
,
则曲线C在点P处的切线的斜率
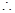 直线PQ的方程为
直线PQ的方程为
取 ,得
,得

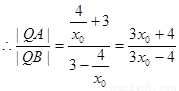 又
又
 ,即PQ平分
,即PQ平分
 PQ恒过点M,得证
PQ恒过点M,得证

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目