题目内容
7．设曲线F1（x，y）=0和F2（x，y）=0的交点为P，那么曲线F1（x，y）-F2（x，y）=0必定（ ）| A． | 经过P点 | B． | 经过原点 | C． | 经过P点和原点 | D． | 不一定经过P点 |
分析 P是曲线F1（x，y）=0和F2（x，y）=0的交点，所以F1（x0，y0）=0，F2（x0，y0）=0．由此得F1（x0，y0）-F2（x0，y0）=0，即可得出结论．
解答 解：设P点的坐标为（x0，y0），则
因为P是曲线F1（x，y）=0和F2（x，y）=0的交点，所以F1（x0，y0）=0，F2（x0，y0）=0．
由此得F1（x0，y0）-F2（x0，y0）=0，故曲线F1（x，y）-F2（x，y）=0经过点P．
故选：A．
点评 本题考查曲线与方程，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
15．5005×50065006-5006×50055005的值是（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 2 |
19．猜测（1-$\frac{4}{1}$）（1-$\frac{4}{9}$）…[1一$\frac{4}{（2n-1）^{2}}$]对n∈N且n≥1成立的-个表达式为 （ ）
| A． | -$\frac{n+2}{n}$ | B． | $\frac{2n+1}{2n-1}$ | C． | $-\frac{2n+1}{2n-1}$ | D． | -$\frac{n+1}{n-1}$ |
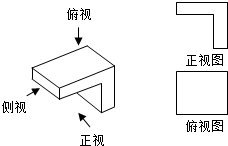在如图中，图（b）是图（a）中实物画出的正视图和俯视图，你认为正确的吗？如果不正确，请找出错误并改正，然后画出侧视图（尺寸不作严格要求）