题目内容
用数学归纳法证明等式: …
…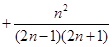 =
=
对于一切 都成立.
都成立.
利用数学归纳法。
解析试题分析:(1)当n=1时,左边=  ,右边=
,右边= ,等式成立。
,等式成立。
(2)假设n=k时,等式成立,即 …
…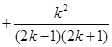 =
= ,
,
那么n=k+1时, ……
……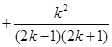
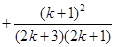
=
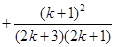
= ,
,
这就是说,当n=k+1时 等式也成了
故对一切 等式都成立。
等式都成立。
考点:本题主要考查数学归纳法。
点评:容易题,利用数学归纳法,可证明与自然数有关的命题,证明过程中,要注意规范写出“两步一结”。

练习册系列答案
相关题目
若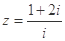 ,则复数
,则复数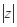 =( )
=( )
A.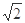 | B.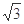 | C.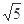 | D.5 |
已知复数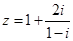 ,则
,则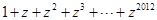 的值为( )
的值为( )
A.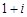 | B.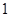 | C.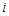 | D.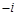 |
已知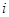 是虚数单位,复数
是虚数单位,复数 的模为( )
的模为( )
A. | B.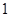 | C. | D.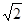 |
复数 =( )
=( )
| A.2+i | B.2-i | C.1+2i | D.1-2i |
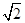 ,
, ,
,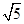 不能为同一等差数列中的三项.
不能为同一等差数列中的三项.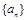 满足
满足 ,
, .
. 、
、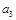 、
、 ;
;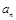 的表达式;
的表达式; ,求
,求 .
. 在点
在点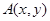 处的切线斜率为
处的切线斜率为 ,且
,且 .对一切实数
.对一切实数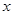 ,不等式
,不等式 恒成立(
恒成立( ≠0).
≠0).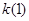 的值;
的值;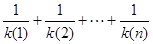 >
> .
.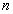 为正整数,试比较
为正整数,试比较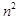 与
与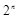 的大小 .
的大小 .