题目内容
在△ABC中,已知角A为锐角,且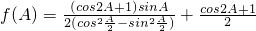 .
.
(1)将f(A)化简成f(A)=Msin(ωA+φ)+N的形式;
(2)若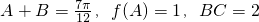 ,求边AC的长.
,求边AC的长.
解:(1)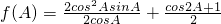 (2分)
(2分)
= (1分)
(1分)
=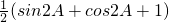 (1分)
(1分)
=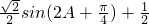 (2分)
(2分)
(2)由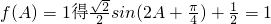 ,∴
,∴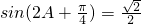 .(2分)
.(2分)
∴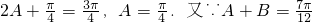 ,∴
,∴ .∴
.∴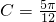 .(A,B,C各(1分)共3分)
.(A,B,C各(1分)共3分)
在△ABC中,由正弦定理得: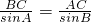 .∴
.∴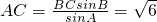 (2分)
(2分)
分析:(1)通过二倍角公式化简分式的分子,分母然后利用两角和的正弦函数即可把函数化简成f(A)=Msin(ωA+φ)+N的形式;
(2)利用f(A)求出A的值,得到B,C的值,利用正弦定理求出AC的值即可.
点评:本题是基础题,考查三角函数的公式的应用,正弦定理的应用,考查计算能力.
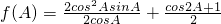 (2分)
(2分)=
 (1分)
(1分)=
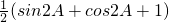 (1分)
(1分)=
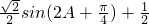 (2分)
(2分)(2)由
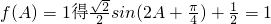 ,∴
,∴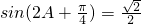 .(2分)
.(2分)∴
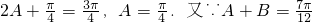 ,∴
,∴ .∴
.∴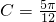 .(A,B,C各(1分)共3分)
.(A,B,C各(1分)共3分)在△ABC中,由正弦定理得:
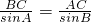 .∴
.∴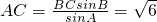 (2分)
(2分)分析:(1)通过二倍角公式化简分式的分子,分母然后利用两角和的正弦函数即可把函数化简成f(A)=Msin(ωA+φ)+N的形式;
(2)利用f(A)求出A的值,得到B,C的值,利用正弦定理求出AC的值即可.
点评:本题是基础题,考查三角函数的公式的应用,正弦定理的应用,考查计算能力.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目