题目内容
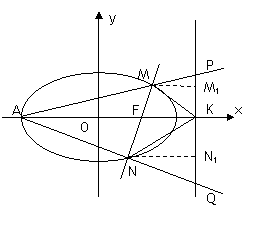
(08年黄冈中学二模理)如图,已知椭圆![]() 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线![]() 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.
(1)求证:KF平分∠MKN;
(2)直线AM、AN分别交准线![]() 于点P、Q,设直线MN的倾斜角为
于点P、Q,设直线MN的倾斜角为![]() ,试用
,试用![]() 表示线段PQ的长度|PQ|,并求|PQ|的最小值.
表示线段PQ的长度|PQ|,并求|PQ|的最小值.

解析:(1)法一:作MM1⊥![]()
![]() 于M1,
于M1,
NN1⊥![]()
![]() 于N1,则
于N1,则![]() ,
,
又由椭圆的第二定义有
![]() ∴
∴![]() ∴∠KMM1=∠KNN1,即∠MKF=∠NKF,
∴∠KMM1=∠KNN1,即∠MKF=∠NKF,
∴KF平分∠MKN
法二:设直线MN的方程为![]() .
.
设M、N的坐标分别为![]() , 由
, 由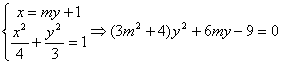
∴![]()
设KM和KN的斜率分别为![]() ,显然只需证
,显然只需证![]() 即可.
即可.
∵![]() ∴
∴![]()
而![]()
![]() 即
即![]() 得证.
得证.
(2)由A,M,P三点共线可求出P点的坐标为![]()
由A,N,Q三点共线可求出Q点坐标为![]() ,
,
设直线MN的方程为![]() .由
.由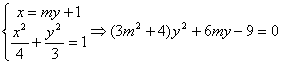
∴![]()
则:![]()
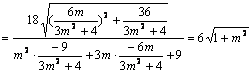
又直线MN的倾斜角为![]() ,则
,则![]() ,∴
,∴![]()
∴![]() 时,
时,![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目