题目内容
3.已知bn=$\frac{n}{n+1}$,Sn=$\frac{n-4}{2(n-2)}$.求实数a为何值时,4a•Sn<bn恒成立.分析 通过Sn=$\frac{n-4}{2(n-2)}$、bn=$\frac{n}{n+1}$易知当n≥5时Sn>0,分n<5、n≥5两种情况讨论即可.
解答 解:∵Sn=$\frac{n-4}{2(n-2)}$,bn=$\frac{n}{n+1}$,
∴S1=$\frac{1-4}{2(1-2)}$=$\frac{3}{2}$,b1=$\frac{1}{1+1}$=$\frac{1}{2}$,S2不存在,
∵4a•Sn<bn恒成立,
∴a<$\frac{{b}_{1}}{4{S}_{1}}$=$\frac{\frac{1}{2}}{4×\frac{3}{2}}$=$\frac{1}{8}$,
∵S3=$\frac{3-4}{2(3-2)}$=-$\frac{1}{2}$,b3=$\frac{3}{3+1}$=$\frac{3}{4}$,
∴a>$\frac{{b}_{3}}{4{S}_{3}}$=$\frac{\frac{3}{4}}{4×(-\frac{1}{2})}$=-$\frac{3}{8}$,
∵S4=$\frac{4-4}{2(4-2)}$=0,b4=$\frac{4}{4+1}$=$\frac{4}{5}$,
∴4a•Sn<bn恒成立,
∵当n≥5时,Sn>0,4a•Sn<bn恒成立,
∴a<$\frac{{b}_{n}}{4{S}_{n}}$=$\frac{\frac{n}{n+1}}{\frac{4(n-4)}{2(n-2)}}$=$\frac{1}{2}$•$\frac{{n}^{2}-2n}{{n}^{2}-3n-4}$恒成立,
∵$\underset{lim}{n→∞}$$\frac{{n}^{2}-2n}{{n}^{2}-3n-4}$=1,
∴a<$\frac{1}{2}$,
综上所述:-$\frac{3}{8}$<a<$\frac{1}{2}$.
点评 本题是一道关于数列与不等式的综合题,涉及极限等基础知识,注意解题方法的积累,属于中档题.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | 42 | B. | 40 | C. | 36 | D. | 53 |
| A. | 36π | B. | 288π | C. | 12π | D. | 18π |
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
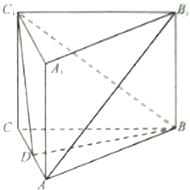 如图,在正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1中,D为AC的中点,
如图,在正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1中,D为AC的中点,