题目内容
(13分)已知圆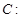
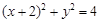 ,相互垂直的两条直线
,相互垂直的两条直线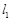 、
、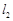 都过点
都过点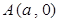 .
.
(Ⅰ)当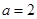 时,若圆心为
时,若圆心为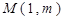 的圆和圆
的圆和圆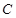 外切且与直线
外切且与直线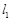 、
、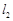 都相切,求圆
都相切,求圆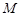 的方程;
的方程;
(Ⅱ)当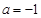 时,求
时,求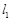 、
、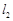 被圆
被圆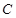 所截得弦长之和的最大值.
所截得弦长之和的最大值.
【答案】
(Ⅰ)圆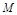 的方程为
的方程为 .
.
(Ⅱ)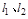 被圆C所截得弦长之和的最大值为
被圆C所截得弦长之和的最大值为
【解析】(Ⅰ)设圆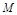 的半径为
的半径为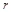 ,则圆心
,则圆心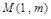 到点
到点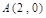 的距离为
的距离为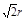 ,
,
∴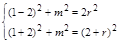 .
.
解得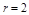 且
且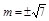 ,∴圆
,∴圆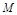 的方程为
的方程为 .
………6分
.
………6分
(Ⅱ)当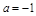 时,设圆
时,设圆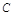 的圆心为
的圆心为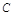 ,
,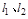 被圆C所截得弦的中点分别为
被圆C所截得弦的中点分别为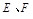 ,弦长分别为
,弦长分别为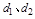 ,
,
因为四边形 是矩形,所以
是矩形,所以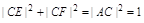 ,即
,即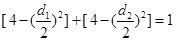 ,
,
化简得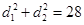 .由
.由 ,∴
,∴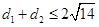 .
.
即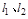 被圆C所截得弦长之和的最大值为
被圆C所截得弦长之和的最大值为 .
………13分
.
………13分

练习册系列答案
相关题目