题目内容
已知圆![]()
![]() ,相互垂直的两条直线
,相互垂直的两条直线![]() 、
、![]() 都过点
都过点![]() .
.
(Ⅰ)当![]() 时,若圆心为
时,若圆心为![]() 的圆和圆
的圆和圆![]() 外切且与直线
外切且与直线![]() 、
、![]() 都相切,求圆
都相切,求圆![]() 的
的
方程;
(Ⅱ)当![]() 时,求
时,求![]() 、
、![]() 被圆
被圆![]() 所截得弦长之和的最大值,并求此时直线
所截得弦长之和的最大值,并求此时直线![]() 的方程.
的方程.
同下
解析:
(Ⅰ)设圆![]() 的半径为
的半径为![]() ,易知圆心
,易知圆心![]() 到点
到点![]() 的距离为
的距离为![]() ,
,
∴ ……………………………………………………………4分
……………………………………………………………4分
解得![]() 且
且![]() ∴圆
∴圆![]() 的方程为
的方程为![]() …………………7分
…………………7分
(Ⅱ)当![]() 时,设圆
时,设圆![]() 的圆心为
的圆心为![]() ,
,![]() 、
、![]() 被圆
被圆![]() 所截得弦的中点分别为
所截得弦的中点分别为![]() ,弦长分别为
,弦长分别为![]() ,因为四边形
,因为四边形![]() 是矩形,所以
是矩形,所以![]() ,即
,即
 ,化简得 …………………………10分
,化简得 …………………………10分
从而![]() ,等号成立
,等号成立![]() ,
,
![]() 时,
时,![]() ,
,
即![]() 、
、![]() 被圆
被圆![]() 所截得弦长之和的最大值为
所截得弦长之和的最大值为![]() …………………………………13分
…………………………………13分
此时![]() ,显然直线
,显然直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为:
的方程为:![]() ,则
,则
![]() ,
,![]() ,
,
∴直线![]() 的方程为:
的方程为:![]() 或
或![]() …………………………15分
…………………………15分

练习册系列答案
相关题目
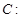
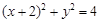 ,相互垂直的两条直线
,相互垂直的两条直线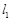 、
、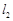 都过点
都过点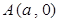 .
.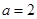 时,若圆心为
时,若圆心为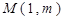 的圆和圆
的圆和圆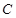 外切且与直线
外切且与直线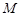 的方程;
的方程;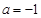 时,求
时,求