题目内容
非零向量 ,则“
,则“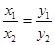 ”是“
”是“ ∥
∥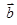 ”的 条件.
”的 条件.
充分不必要;
解析试题分析:若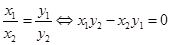 ,则
,则 ∥
∥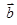 ;
;
若 ∥
∥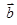 ,则
,则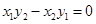 ,若
,若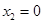 或
或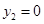 时
时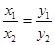 不一定成立;故“
不一定成立;故“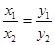 ”是“
”是“ ∥
∥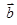 ”的充分不必要条件.
”的充分不必要条件.
考点:1.向量共线的坐标表示;2.充分必要条件的判断.

练习册系列答案
相关题目
题目内容
非零向量 ,则“
,则“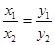 ”是“
”是“ ∥
∥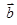 ”的 条件.
”的 条件.
充分不必要;
解析试题分析:若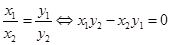 ,则
,则 ∥
∥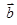 ;
;
若 ∥
∥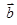 ,则
,则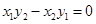 ,若
,若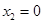 或
或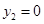 时
时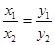 不一定成立;故“
不一定成立;故“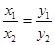 ”是“
”是“ ∥
∥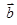 ”的充分不必要条件.
”的充分不必要条件.
考点:1.向量共线的坐标表示;2.充分必要条件的判断.
