题目内容
设三角形△ABC的内角A、B、C所对的边长为a、b、c，且acosB=3，bsinA=4。
（1）求边长a；
（2）若△ABC的面积S=10，求△ABC的周长l的值。
（1）求边长a；
（2）若△ABC的面积S=10，求△ABC的周长l的值。
解：（1）依题设得
，
由正弦定理得：
，所以
，
，即
，
依题设知a2cos2B=9，所以a2=25，得a=5。
（2）因为
，
所以由S=10，得c=5，应用余弦定理得
，
故三角形ABC的周长L=a+b+c=2(5+
)。
，由正弦定理得：
，所以，，即，依题设知a2cos2B=9，所以a2=25，得a=5。
（2）因为
，所以由S=10，得c=5，应用余弦定理得
，故三角形ABC的周长L=a+b+c=2(5+
)。
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
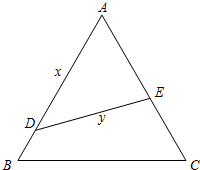如图，公园内有一块边长为2a的正三角形ABC空地，拟改建成花园，并在其中建一直道DE方便花园管理．设D、E分别在AB、AC上，且DE均分三角形ABC的面积．