题目内容
5.已知函数f(x)=2x+k•2-x,k∈R①若函数f(x)为奇函数,求实数k的值.
②若k>0时f(x)min=2,求函数g(x)=ksinx+cosx的值域.
对任意的x∈[0,+∞)都有f(x)>2-x成立,求实数k的取值范围.
分析 ①由函数f(x)为奇函数知f(0)=1+k=0,从而求k=-1,再代入原函数验证为奇函数即可;
②由k>0时f(x)min=2求得k值,代入g(x)=ksinx+cosx后利用辅助角公式化积得答案;把f(x)=2x+k•2-x代入f(x)>2-x,分离参数k后求得答案.
解答 解:①∵f(x)=2x+k•2-x为奇函数,
∴f(0)=1+k=0,解得k=-1.
经检验,f(x)=2x-2-x是奇函数.
故k=-1;
②当k>0时,由f(x)=2x+k•2-x≥$2\sqrt{{2}^{x}•k•{2}^{-x}}=2\sqrt{k}$=2,
得k=1,
∴g(x)=ksinx+cosx=sinx+cosx=$\sqrt{2}sin(x+\frac{π}{4})$.
∴函数g(x)的值域为[$-\sqrt{2},\sqrt{2}$];
对任意的x∈[0,+∞)都有f(x)>2-x成立,即
2x+k•2-x>2-x都成立,
也就是(1-k)•2-x<2x都成立,
∴1-k<(2x)2,
∵x∈[0,+∞),∴(2x)2≥1,
则1-k<1,即k>0.
∴实数k的取值范围是(0,+∞).
点评 本题考查指数函数的性质,考查了三角函数最值的求法,训练了恒成立问题的解决方法,是中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
14.已知{an}是公比小于1的等比数列,且a2=2,a1+a3=5,设Tn=a1a2+a2a3+a3a4+…+anan+1,则( )
| A. | 12≤Tn<16 | B. | 8≤Tn<16 | C. | 12≤Tn<$\frac{32}{3}$ | D. | 8≤Tn<$\frac{32}{3}$ |
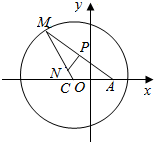 如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.
如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.