题目内容
已知各项都是正数的等比数列{an}的公比q≤1,且a4,a6,-a5成等差数列,则
=( )
| a4+a6 |
| a3+a5 |
分析:由等比数列{an}中,a4,a6,-a5成等差数列,利用等差数列的性质列出关系式,再利用等比数列的通项公式化简后,得到关于q的方程,求出方程的解得到q的值,然后将所求式子的分子利用等比数列的性质化简后约分,将q的值代入即可求出值.
解答:解:∵等比数列{an}中,a4,a6,-a5成等差数列,
∴2a6=a4-a5,即2a1q5=a1q3-a1q4,
∵a1≠0,q≠0,
∴2q2+q-1=0,即(2q-1)(q+1)=0,
解得:q=
或q=-1,
由等比数列{an}各项都为正数,得到q>0,
∴q=
,
则
=
=q=
.
故选C
∴2a6=a4-a5,即2a1q5=a1q3-a1q4,
∵a1≠0,q≠0,
∴2q2+q-1=0,即(2q-1)(q+1)=0,
解得:q=
| 1 |
| 2 |
由等比数列{an}各项都为正数,得到q>0,
∴q=
| 1 |
| 2 |
则
| a4+a6 |
| a3+a5 |
| q(a3+a5) |
| a3+a5 |
| 1 |
| 2 |
故选C
点评:此题考查了等差数列的性质,以及等比数列的通项公式,熟练掌握性质及公式是解本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈ ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是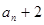 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈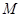 ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 是an+2 和an的等比中项.
是an+2 和an的等比中项. +
+ +…+
+…+ <1;
<1; 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个?