题目内容
已知F是椭圆 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线 相切.
相切.(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在过F作斜率为k(k≠0)的直线l交椭圆于M,N两点,P为线段MN的中点,设O为椭圆中心,射线OP交椭圆于点Q,若
 ,若存在求k的值,若不存在则说明理由.
,若存在求k的值,若不存在则说明理由.
【答案】分析:(Ⅰ)先确定出F,A的坐标,进而确定点B的坐标,从而可确定A,B,F三点确定的圆的圆心坐标与半径,利用圆与直线相切,即可求椭圆的方程;
(Ⅱ)假设存在,设直线l的方程为:y=k(x+1)代入椭圆的方程 ,根据P为线段MN的中点,确定P的坐标,进而可得Q的坐标,代入椭圆方程,即可判断k不存在.
,根据P为线段MN的中点,确定P的坐标,进而可得Q的坐标,代入椭圆方程,即可判断k不存在.
解答:解:(Ⅰ)∵椭圆的离心率为 ,∴
,∴ ,∴
,∴
∴ ,
,
∵AB⊥AF,∴
∴AB的方程为:
令y=0,∴ ,∴
,∴
∴A,B,F三点确定的圆的圆心坐标为 ,半径为r=a
,半径为r=a
∴圆心到直线 的距离为
的距离为 ,
,
∵A,B,F三点确定的圆C恰好与直线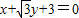 相切.
相切.
∴
∴a=2,∴
∴椭圆的方程为 ;
;
(Ⅱ)假设存在,设直线l的方程为:y=k(x+1)代入椭圆的方程 ,消去y可得
,消去y可得
(3+4k2)x2+8k2x+(4k2-12)=0
设M(x1,y1),N(x2,y2),Q(x,y),则 ,
,
∵P为线段MN的中点,∴
∴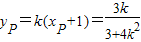
∵ ,∴
,∴
∴
∵射线OP交椭圆于点Q
∴
∴
∴64k4+48k2=4(16k4+24k2+9)
∴48k2=96k2+36
∴-48k2=36
此方程无解,∴k不存在.
点评:本题考查圆与圆锥曲线的综合,考查椭圆的标准方程,考查直线与圆相切,考查代入法的运用,解题的关键是确立动点坐标之间的关系,有综合性.
(Ⅱ)假设存在,设直线l的方程为:y=k(x+1)代入椭圆的方程
 ,根据P为线段MN的中点,确定P的坐标,进而可得Q的坐标,代入椭圆方程,即可判断k不存在.
,根据P为线段MN的中点,确定P的坐标,进而可得Q的坐标,代入椭圆方程,即可判断k不存在.解答:解:(Ⅰ)∵椭圆的离心率为
 ,∴
,∴ ,∴
,∴
∴
 ,
,∵AB⊥AF,∴

∴AB的方程为:

令y=0,∴
 ,∴
,∴
∴A,B,F三点确定的圆的圆心坐标为
 ,半径为r=a
,半径为r=a∴圆心到直线
 的距离为
的距离为 ,
,∵A,B,F三点确定的圆C恰好与直线
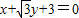 相切.
相切.∴

∴a=2,∴

∴椭圆的方程为
 ;
;(Ⅱ)假设存在,设直线l的方程为:y=k(x+1)代入椭圆的方程
 ,消去y可得
,消去y可得(3+4k2)x2+8k2x+(4k2-12)=0
设M(x1,y1),N(x2,y2),Q(x,y),则
 ,
,∵P为线段MN的中点,∴

∴
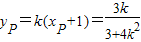
∵
 ,∴
,∴
∴

∵射线OP交椭圆于点Q
∴

∴

∴64k4+48k2=4(16k4+24k2+9)
∴48k2=96k2+36
∴-48k2=36
此方程无解,∴k不存在.
点评:本题考查圆与圆锥曲线的综合,考查椭圆的标准方程,考查直线与圆相切,考查代入法的运用,解题的关键是确立动点坐标之间的关系,有综合性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线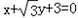 相切.
相切. ,若存在求k的值,若不存在则说明理由.
,若存在求k的值,若不存在则说明理由. 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线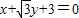 相切.
相切.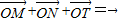 ,如果存在,则求点T的坐标;如果不存在,请说明理由.
,如果存在,则求点T的坐标;如果不存在,请说明理由.
 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线 相切.
相切. 成立.如果存在,则求k的值;如果不存在,请说明理由.
成立.如果存在,则求k的值;如果不存在,请说明理由.