题目内容
已知F是椭圆 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线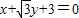 相切.
相切.(1)求椭圆的方程;
(2)设O为椭圆的中心,过F点作直线交椭圆于M、N两点,在椭圆上是否存在点T,使得
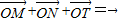 ,如果存在,则求点T的坐标;如果不存在,请说明理由.
,如果存在,则求点T的坐标;如果不存在,请说明理由.
【答案】分析:(1)利用椭圆的离心率为 ,可得A,F的坐标,从而可求AF的斜率,进而可得AB的斜率与方程,由此可得圆心坐标与半径,利用A、B、F三点确定的圆C恰好与直线
,可得A,F的坐标,从而可求AF的斜率,进而可得AB的斜率与方程,由此可得圆心坐标与半径,利用A、B、F三点确定的圆C恰好与直线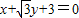 相切,即可求得椭圆方程;
相切,即可求得椭圆方程;
(2)分类讨论,将直线方程代入椭圆方程,利用向量知识及韦达定理,即可求得结论.
解答:解:(1)∵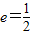 ,∴
,∴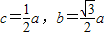
∴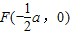
取A(0,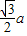 ),∴
),∴
∵AB⊥AF,∴ ,∴
,∴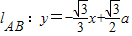
令y=0,∴ ,∴
,∴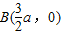
∴圆心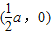 ,半径r=a
,半径r=a
∵A、B、F三点确定的圆C恰好与直线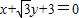 相切
相切
∴圆心到直线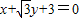 的距离
的距离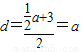 ,∴a=2,∴
,∴a=2,∴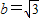
∴椭圆方程为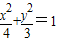 …(7分)
…(7分)
(2)当MN的斜率存在时,设直线MN:ny=x+1,联立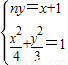 ,(3n2+4)y2-6ny-9=0,
,(3n2+4)y2-6ny-9=0,
设M(x1,y1),N(x2,y2),T(x,y),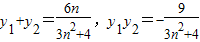
∵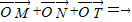 ,
,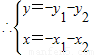
∴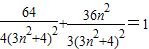 ,解得,n=0.…(12分)
,解得,n=0.…(12分)
即MN的斜率存在时,T(2,0).
当MN的斜率为0时,T不存在. …(14分)
点评:本题考查椭圆的标准方程,考查直线与圆的位置关系,考查向量知识的运用,考查韦达定理的运用,解题的关键是直线与椭圆方程联立,利用韦达定理及向量知识,建立方程.
 ,可得A,F的坐标,从而可求AF的斜率,进而可得AB的斜率与方程,由此可得圆心坐标与半径,利用A、B、F三点确定的圆C恰好与直线
,可得A,F的坐标,从而可求AF的斜率,进而可得AB的斜率与方程,由此可得圆心坐标与半径,利用A、B、F三点确定的圆C恰好与直线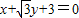 相切,即可求得椭圆方程;
相切,即可求得椭圆方程;(2)分类讨论,将直线方程代入椭圆方程,利用向量知识及韦达定理,即可求得结论.
解答:解:(1)∵
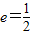 ,∴
,∴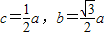
∴
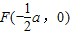
取A(0,
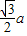 ),∴
),∴
∵AB⊥AF,∴
 ,∴
,∴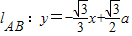
令y=0,∴
 ,∴
,∴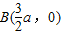
∴圆心
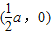 ,半径r=a
,半径r=a∵A、B、F三点确定的圆C恰好与直线
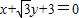 相切
相切∴圆心到直线
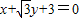 的距离
的距离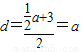 ,∴a=2,∴
,∴a=2,∴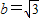
∴椭圆方程为
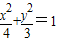 …(7分)
…(7分)(2)当MN的斜率存在时,设直线MN:ny=x+1,联立
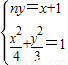 ,(3n2+4)y2-6ny-9=0,
,(3n2+4)y2-6ny-9=0,设M(x1,y1),N(x2,y2),T(x,y),
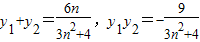
∵
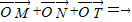 ,
,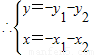
∴
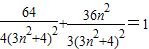 ,解得,n=0.…(12分)
,解得,n=0.…(12分)即MN的斜率存在时,T(2,0).
当MN的斜率为0时,T不存在. …(14分)
点评:本题考查椭圆的标准方程,考查直线与圆的位置关系,考查向量知识的运用,考查韦达定理的运用,解题的关键是直线与椭圆方程联立,利用韦达定理及向量知识,建立方程.

练习册系列答案
相关题目
 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线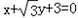 相切.
相切. ,若存在求k的值,若不存在则说明理由.
,若存在求k的值,若不存在则说明理由. 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A,B,F三点确定的圆C恰好与直线 相切.
相切. ,若存在求k的值,若不存在则说明理由.
,若存在求k的值,若不存在则说明理由. 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线 相切.
相切. 成立.如果存在,则求k的值;如果不存在,请说明理由.
成立.如果存在,则求k的值;如果不存在,请说明理由.