题目内容
已知双曲线![]() 的左、右顶点分别为A、B,右焦点为F(c,0)(c>0),右准线为
的左、右顶点分别为A、B,右焦点为F(c,0)(c>0),右准线为![]() ,|AF|=3.过点F作直线交双曲线的右支于P,Q两点,延长PB交右准线l于M点.
,|AF|=3.过点F作直线交双曲线的右支于P,Q两点,延长PB交右准线l于M点.
(Ⅰ)求双曲线的方程;
(Ⅱ)若![]() ,求△PBQ的面积S;
,求△PBQ的面积S;
(Ⅲ)(理)若![]() (λ≠0,λ≠-1),问是否存在实数μ=f(λ),使得:
(λ≠0,λ≠-1),问是否存在实数μ=f(λ),使得:![]() .若存在,求出μ=f(λ)的表达式;若不存在,请说明理由.
.若存在,求出μ=f(λ)的表达式;若不存在,请说明理由.
(文)若![]() ,问是否存在实数μ,使得:
,问是否存在实数μ,使得:![]() .若存在,求出μ的值;若不存在,请说明理由.
.若存在,求出μ的值;若不存在,请说明理由.
答案:
解析:
解析:
|
(Ⅰ)由题意知 (Ⅱ)设 可设PQ方程为:y=k(x-2). 代入双曲线方程可得: 由于P、Q都在双曲线的右支上,所以,
∴ 由于 由 由此 ∴ ∴
(Ⅲ)(理)存在实数μ满足题设条件. ∵PB的直线方程为: 即 ∵ ∴ 即 又∵ 把③④代入②得: 由①⑤得: ∴
令 ∴ 故存在实数μ,满足题设条件. (文)存在实数μ,满足题设条件, ∵PB的直线方程为: 即 ∵ ∴ 即 又∵ 把③④代入②得: 由①⑤得: 又∵ ∴
即 则存在实数 |

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
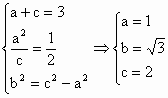 ,则双曲线方程为:
,则双曲线方程为: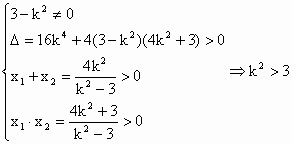 .
.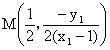 ,
,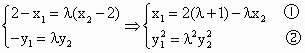
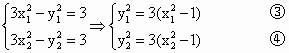

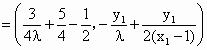
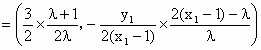
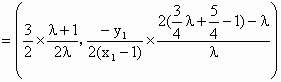
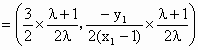
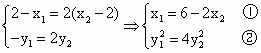
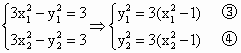
 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.  与
与 交点的轨迹E的方程
交点的轨迹E的方程 的两条直线
的两条直线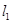 和
和 与轨迹E都只有一个交点,且
与轨迹E都只有一个交点,且 ,求
,求 的值.
的值. 分)
分) 的左、 右顶点分别为
的左、 右顶点分别为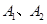 ,动直线
,动直线 与圆
与圆 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为 .
.
 的取值范围,并求
的取值范围,并求 的最小值;
的最小值; 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,那么,
,那么, 是定值吗?并证明
是定值吗?并证明 的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P, ,则
,则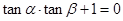 B、
B、
 D、
D、
 的左、右顶点分别为
的左、右顶点分别为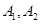 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.  与
与 交点的轨迹E的方程
交点的轨迹E的方程 和
和 与轨迹E都只有一个公共点,且
与轨迹E都只有一个公共点,且 ,求
,求 的值.
的值. 的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P, ,则
( )
,则
( ) B.
B.
 D.
D.