题目内容
已知集合A={x|x=a0+a1×3+a2×32+a3×33},其中ak∈{0,1,2}(k=0,1,2,3),且a3≠0,则A中所有元素之和等于( )
| A.3 240 | B.3 120 |
| C.2 997 | D.2 889 |
D
可利用排除法,若a3也可以取0,则a0,a1,a2,a3都可取0,1,2,根据分步乘法计数原理,可知这样的数共有3×3×3×3=81(个),显然0,1,2这3个数字每个数字要重复27次,故这些元素的和为27×(3+3×3+3×32+3×33)=27×120=3 240;
当a3=0时,a0,a1,a2可取0,1,2,根据分步乘法计数原理,可知这样的数共有3×3×3=27(个),而0,1,2这3个数字每个数字要重复9次,故这些元素的和为9×(3+3×3+3×32)=9×39=351.
所以集合A中所有元素的和为3 240-351=2 889.
当a3=0时,a0,a1,a2可取0,1,2,根据分步乘法计数原理,可知这样的数共有3×3×3=27(个),而0,1,2这3个数字每个数字要重复9次,故这些元素的和为9×(3+3×3+3×32)=9×39=351.
所以集合A中所有元素的和为3 240-351=2 889.

练习册系列答案
相关题目
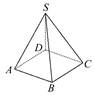
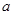 、
、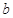 、
、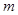 为整数
为整数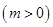 ,若
,若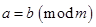 .若
.若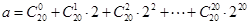 ,且
,且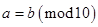 ,则
,则