题目内容
(理)若随机变量的分布列如下表,则Eξ的值为( )
|
分析:先由离散型随机变量分布列的性质知2x+3x+7x+2x+3x+x=1,得到x=
.再由离散型随机变量的数学期望的计算法则能求出Eξ.
| 1 |
| 18 |
解答:解:由题设知:2x+3x+7x+2x+3x+x=1,
解得x=
.
∴Eξ=0×2x+1×3x+2×7x+3×2x+4×3x+5x
=40x
=40×
=
.
故选C.
解得x=
| 1 |
| 18 |
∴Eξ=0×2x+1×3x+2×7x+3×2x+4×3x+5x
=40x
=40×
| 1 |
| 18 |
=
| 20 |
| 9 |
故选C.
点评:本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,注意离散型随机变量分布列的性质的灵活运用.

练习册系列答案
相关题目
 ,x(x>
,x(x>
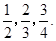
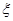 表示乙投篮3次的进球数,求随机变量
表示乙投篮3次的进球数,求随机变量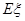 .
.