题目内容
(08年浙江卷理)(本题14分)一个袋中有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是![]() ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是![]() .
.
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为![]() ,求随机变量
,求随机变量![]() 的数学期望
的数学期望![]() .
.
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于![]() .并指出袋中哪种颜色的球个数最少.
.并指出袋中哪种颜色的球个数最少.
本题主要考查排列组合、对立事件、相互独立事件的概率和随机变量分布列和数学期望
等概念,同时考查学生的逻辑思维能力和分析问题以及解决问题的能力.满分14分.
(Ⅰ)解:(i)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,
设袋中白球的个数为![]() ,则
,则![]() ,
,
得到![]() .故白球有5个.
.故白球有5个.
(ii)随机变量![]() 的取值为0,1,2,3,分布列是
的取值为0,1,2,3,分布列是
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的数学期望
的数学期望
![]() .
.
(Ⅱ)证明:设袋中有![]() 个球,其中
个球,其中![]() 个黑球,由题意得
个黑球,由题意得![]() ,
,
所以![]() ,
,![]() ,故
,故![]() .
.
记“从袋中任意摸出两个球,至少有1个黑球”为事件B,则
![]()
![]() .
.
所以白球的个数比黑球多,白球个数多于![]() ,红球的个数少于
,红球的个数少于![]() .
.
故袋中红球个数最少.

练习册系列答案
相关题目
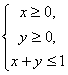 时,恒有
时,恒有