题目内容
在等差数列 中,
中,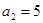 ,
,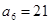 ,记数列
,记数列 的前
的前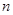 项和为
项和为 ,若
,若 对
对 恒成立,则正整数
恒成立,则正整数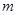 的最小值为( )
的最小值为( )
| A.5 | B.4 | C.3 | D.2 |
A
解析试题分析:由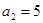 ,
,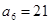 易得等差数列
易得等差数列 的通项公式为
的通项公式为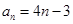 ,所以
,所以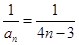 ,故
,故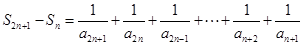 ,设
,设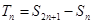 ,则
,则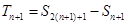
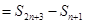 .所以
.所以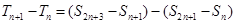
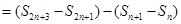
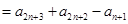
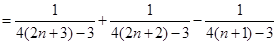
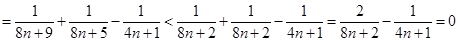 .所以
.所以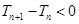 ,即
,即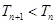 .故
.故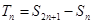 随
随 的增大而减小.所以若
的增大而减小.所以若 对
对 恒成立,即
恒成立,即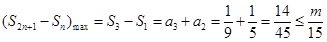 .由
.由 得
得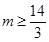 ,所以正整数
,所以正整数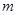 的最小值为5.
的最小值为5.
考点:等差数列的性质、数列的单调性

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
等差数列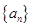 的前n项和为
的前n项和为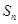 ,且
,且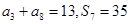 ,则
,则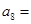 ( )
( )
| A.8 | B.9 | C.1 0 | D.11 |
等差数列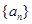 的前
的前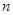 项和为
项和为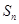 ,且
,且 ,则公差
,则公差 等于( )
等于( )
A.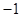 | B.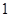 | C. | D. |
已知 为等差数列,且
为等差数列,且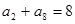 ,
,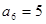 ,则Sl0的值为
,则Sl0的值为
| A.50 | B.45 | C.55 | D.40 |
如果等差数列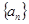 中,
中, ,那么
,那么 等于( )
等于( )
| A.21 | B.30 | C.35 | D.40 |
已知等差数列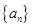 中,
中,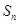 为其前n项和,若
为其前n项和,若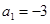 ,
,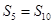 ,则当
,则当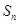 取到最小值时n的值为( )
取到最小值时n的值为( )
| A.5 | B.7 | C.8 | D.7或8 |
等差数列{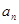 }的公差不为零,首项
}的公差不为零,首项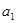 =1,
=1,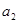 是
是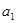 和
和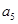 的等比中项,则数列的前10项之和是( )
的等比中项,则数列的前10项之和是( )
| A.90 | B.100 | C.145 | D.190 |
等比数列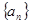 的前
的前 项和为
项和为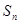 ,若
,若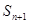 ,
,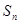 ,
,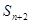 成等差数列,则其公比
成等差数列,则其公比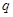 为 ( )
为 ( )
A.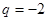 | B.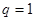 | C.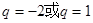 | D. |
已知等比数列{an}的公比为q,记bn=am(n-1)+1+am(n-1)+2+…+am(n-1)+m,cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m(m,n∈N*),则以下结论一定正确的是( )
| A.数列{bn}为等差数列,公差为qm |
| B.数列{bn}为等比数列,公比为q2m |
| C.数列{cn}为等比数列,公比为qm2 |
| D.数列{cn}为等比数列,公比为qmn |