题目内容
定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b= mq
-np,下面说法错误的是( )
| A.若a与b共线,则a⊙b =0 | B.a⊙b =b⊙a |
C.对任意的 R,有( R,有( a)⊙b = a)⊙b = (a⊙b) (a⊙b) | D.(a⊙b)2+(a·b)2= |a|2|b|2 |
B
解析试题分析:由定义知:a⊙b= mq-np:所以选项A正确;又b⊙a=pn-mq≠a⊙b= mq-np,
所以选项B错误;( a)⊙b=
a)⊙b= ,
, (a⊙b)=
(a⊙b)=  ( mq-np)=
( mq-np)= ,所以
,所以
对任意的 R,有(
R,有( a)⊙b =
a)⊙b = (a⊙b),选项C正确;(a⊙b)2+(a·b)2="(" mq-np)2+( mp+nq)2=
(a⊙b),选项C正确;(a⊙b)2+(a·b)2="(" mq-np)2+( mp+nq)2=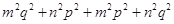 ,|a|2|b|2=
,|a|2|b|2=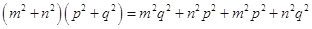 ,
,
所以(a⊙b)2+(a·b)2= |a|2|b|2,因此D正确。
考点:向量的数量积运算;向量的数量积的有关性质。
点评:本题考查向量的数量积的运算,解题时要注意新定义运算的灵活运用,合理地运用平面向量数量积的有关性质进行解题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知正三角形 的边长为1,点
的边长为1,点 是
是 边上的动点,点
边上的动点,点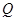 是
是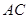 边上的动点,且
边上的动点,且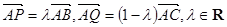 ,则
,则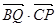 的最大值为
的最大值为
A.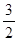 | B.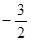 | C.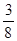 | D.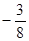 |
已知 则
则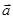 在
在 方向上的投影是( )
方向上的投影是( )
| A.1 | B.-1 | C. | D. |
对任意两个非零的平面向量 和
和 ,定义
,定义 .若平面向量
.若平面向量 ,
, 满足
满足 ,
, 与
与 的夹角
的夹角
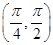 ,且
,且 和
和 都在集合
都在集合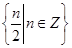 中,则
中,则 =( )
=( )
A. | B. | C.1 | D. |
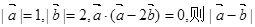 = ( )
= ( )
| A.2 | B.4 | C.1 | D.8 |
下列命题中正确的是 ( )
A.若 , , ,则 ,则 |
B.若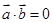 ,则 ,则 与 与 中至少有一个为 中至少有一个为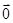 |
C.对于任意向量  , , , , ,有 ,有 |
D.对于任意向量 ,有 ,有 |
已知平面上 三点共线,且
三点共线,且 ,则对于函数
,则对于函数 ,下列结论中错误的是( )
,下列结论中错误的是( )
A.周期是 | B.最大值是2 |
C. 是函数的一个对称点 是函数的一个对称点 | D.函数在区间 上单调递增 上单调递增 |
在△ABC中,D为BC边上的点, =
=
 +
+
 ,则
,则 的最大值为
的最大值为
| A.1 | B. | C. | D. |
 ,
,  , 且
, 且 , 则
, 则 等于 ( )
等于 ( )